Inference

EC 320 - Introduction to Econometrics

Jose Rojas-Fallas

2025

Prologue

OLS

Up to now, we have been focusing on OLS considering:

• How we model regressions with this estimator
• How the estimator is derived and what properties it demonstrates
• How the classical assumptions make the estimator BLUE

We have mostly ignored drawing conclusions about the true population parameters from the estimates of the sample data

This is inference

OLS

Thus far we have fit an OLS model to find an answer to the following questions:

• How much does an additional year of schooling increase earnings?
• Does the number of police officers affect campus crime rates?

Up to now, we have not discussed our confidence in our fitted relationship

Even if all 6 Assumptions hold, sample selection might generate the incorrect conclusions in a completely unbiased, coincidental fashion.

Previously we used the first 3 assumptions to show that OLS is unbiased:

\[ \mathop{\mathbb{E}}\left[ \hat{\beta} \right] = \beta \]

We used the first 5 assumptions to derive a formula for the variance of the OLS estimator:

\[ \mathop{\text{Var}}(\hat{\beta}) = \frac{\sigma^2}{\sum_{i=1}^n (X_i - \bar{X})^2} \]

By using the variance of the OLS estimator, we can infer confidence from the sampling distribution

Sampling distribution

The probability distribution of the OLS estimators obtained from repeatedly drawing random samples of the same size from a population and fitting point estimates each time.

Provides information about their variability, accuracy, and precision across different samples.

Point estimates

The fitted values of the OLS estimator (e.g., \(\hat{\beta}_0, \hat{\beta}_1\))

Sampling distribution properties

1. Unbiasedness: If the Gauss-Markov assumptions hold, the OLS estimators are unbiased (i.e., \(E(\hat{\beta}_0) = \beta_0\) and \(E(\hat{\beta}_1) = \beta_1\))

2. Variance: The variance of the OLS estimators describes their dispersion around the true population parameters.

3. Normality: If the errors are normally distributed or the sample size is large enough, by the Central Limit Theorem, the sampling distribution of the OLS estimators will be approximately normal.¹

1. Useful for making inferences, constructing confidence intervals, and performing hypothesis tests using the t-distribution.

Sampling distribution

The sampling distribution of \(\hat{\beta}\) to conduct hypothesis tests.

Use all 6 classical assumptions to show that OLS is normally distributed:

\[ \hat{\beta} \sim \mathop{N}\left( \beta, \frac{\sigma^2}{\sum_{i=1}^n (X_i - \bar{X})^2} \right) \]

Let’s look at a simulation

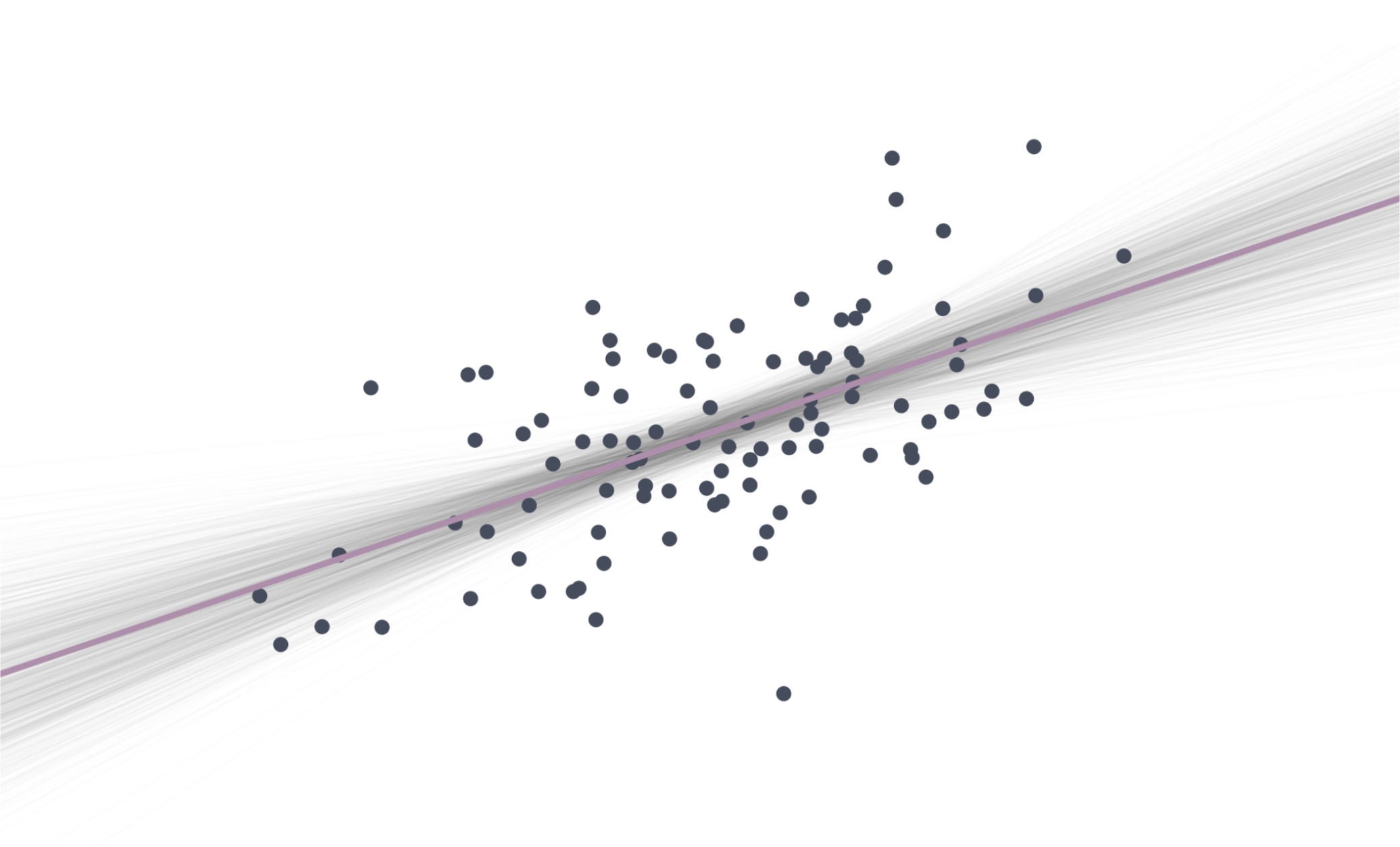
Plotting the distributions of the point estimates in a histogram

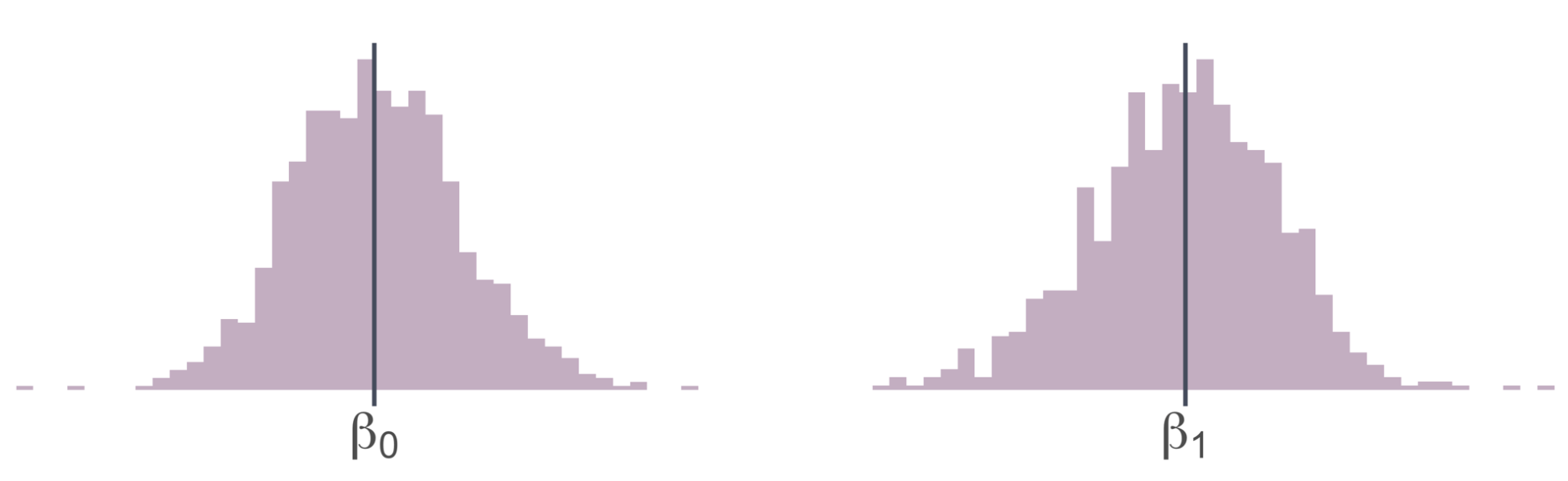
Simulating 1,000 draws

Plotting the distributions of the point estimates in a histogram

Simulating 10,000 draws

Inference

Inference

Our current workflow consists of:

1. Get data (points with \(X\) and \(Y\) values)
2. Regress \(Y\) on \(X\) (aka \(Y = \beta_{0} + \beta_{1}X\))
3. Plot the point estimates \((\hat{\beta}_{0},\hat{\beta}_{1})\) and report them

But when do we learn something? We are still missing a step.

• For \(\hat{\beta}_{1}\), can we rule out a previously hypothesized values?
• How condifent should we be in the precision of our estimates?

We need to be careful about our sample being atypical \(\Rightarrow\) uncertainty

However, there is a problem.

Recall the variance of the point estimate \(\hat{\beta_1}\) \[ \mathop{\text{Var}}(\hat{\beta}_1) = \frac{\sigma^2}{\sum_{i=1}^n (X_i - \bar{X})^2} \]

The problem is that \(\color{#BF616A}{\sigma^2}\) is unobserved. So what do we do? Estimate it.

Estimating error variance

We can estimate the variance of \(u_i\) (\(\color{#BF616A}{\sigma^2}\)) using the sum of squared residuals (RSS):

\[ s^2_u = \dfrac{\sum_i \hat{u}_i^2}{n - k} \]

where \(n\) is the number of observations and \(k\) is the number of regression parameters. (In a simple linear regression, \(k=2\))

If the assumptions from Gauss-Markov hold, then \(s^2_u\) is an unbiased estimator of \(\sigma^2\).

In essence, we are learning from our prediction errors

OLS Variance

With \(s^2_u = \dfrac{\sum_i \hat{u}_i^2}{n - k}\), we can calculate the estimated variance of \(\hat{\beta}_1\)

\[ \mathop{\text{Var}}(\hat{\beta}_1) = \frac{s^2_u}{\sum_{i=1}^n (X_i - \bar{X})^2} \]

Taking the square root, we get the standard error of the OLS estimator:

\[ \mathop{\widehat{\text{SE}}} \left( \hat{\beta}_1 \right) = \sqrt{ \frac{s^2_u}{\sum_{i=1}^n (X_i - \bar{X})^2} } \]

The standard error is the standard deviation of the sampling distribution.

Inference

After deriving the distribution of \(\hat{\beta}_1\)¹, we have two (related) options for formal statistical inference (learning) about our unknown parameter \(\beta_1\):

• Hypothesis testing: Determine whether there is statistically significant evidence to reject a hypothesized value or range of values.
• Confidence intervals: Use the estimate and its standard error to create an interval that will generally² contain the true parameter.

1. Hint: It’s normal with mean \(\beta_1\) and variance \(\frac{\sigma^2}{\sum_{i=1}^n (X_i - \bar{X})^2}\).

2. E.g., similarly constructed 95% confidence intervals will contain the true parameter 95% of the time.

Hypothesis Testing

Hypothesis Tests

Systematic procedure that gives us evidence to hang our hat on. Starting with a Null hypothesis (\(H_0\)) and an Alternative hypothesis (\(H_1\))

\[ \begin{align*} H_0:& \beta_1 = 0 \\ H_1:& \beta_1 \neq 0 \end{align*} \]

In the context of the wage regression:

\[ \text{Wage}_i = \beta_0 + \beta_1 \cdot \text{Education}_i + u_i \]

\(H_0\): Education has no effect on wage

\(H_1\): Education has an effect on wage

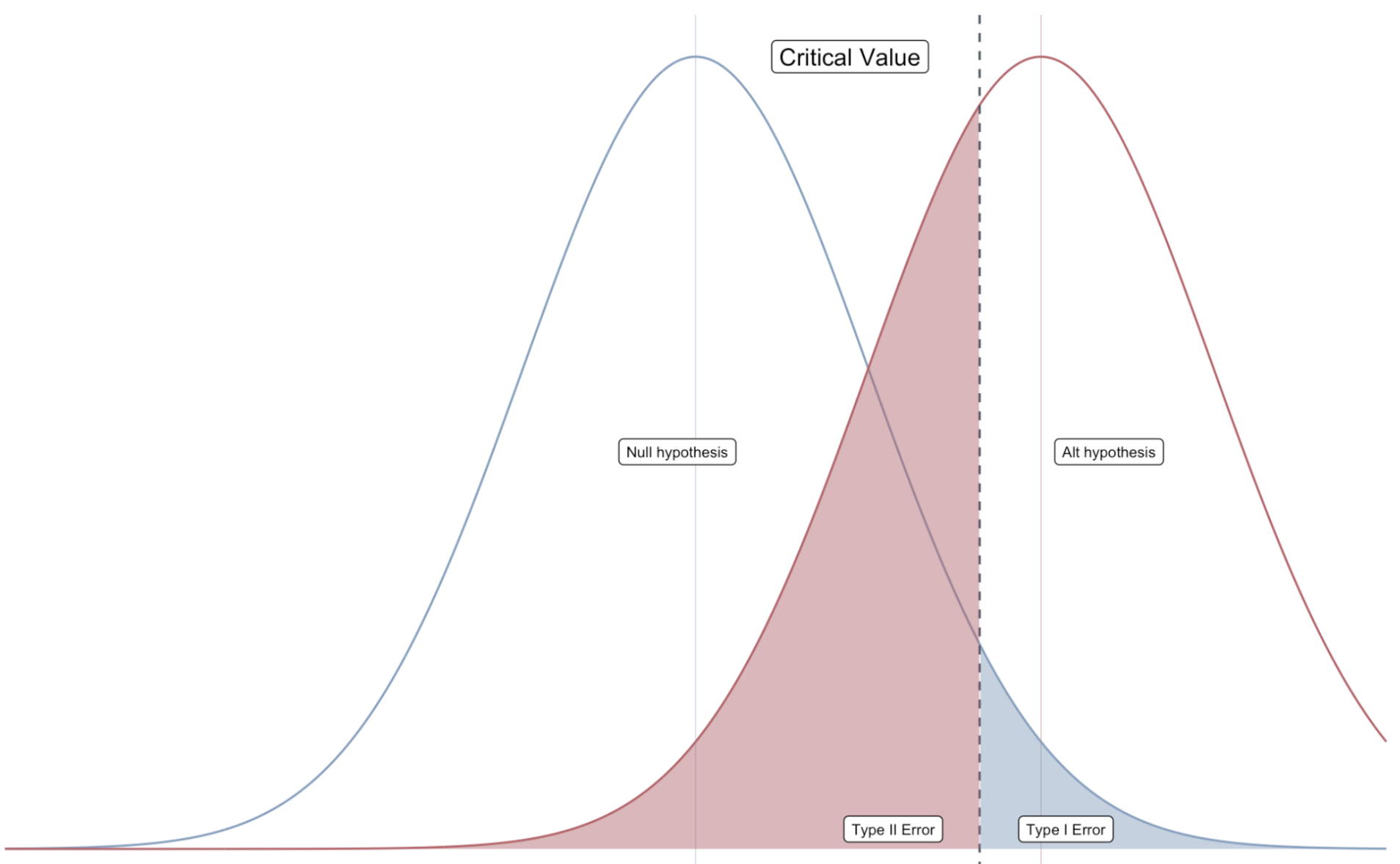
Possible outcomes

Within this structure, four possible outcomes exist:

1. We fail to reject the null hypothesis and the null is true.

Ex. Education has no effect on wage and, correctly, we fail to reject \(H_0\).

Possible outcomes

Within this structure, four possible outcomes exist:

1. We fail to reject the null hypothesis and the null is true.

2. We reject the null hypothesis and the null is false.

Ex. Education has an effect on wage and, correctly, we reject \(H_0\).

Possible outcomes

Within this structure, four possible outcomes exist:

1. We fail to reject the null hypothesis and the null is true.

2. We reject the null hypothesis and the null is false.

3. We reject the null hypothesis, but the null is actually true.

Ex. Education has no effect on wage, but we incorrectly reject \(H_0\).

This is an error. Defined as a Type I error.

Possible outcomes

Within this structure, four possible outcomes exist:

1. We fail to reject the null hypothesis and the null is true.

2. We reject the null hypothesis and the null is false.

3. We reject the null hypothesis, but the null is actually true.

4. We fail to reject the null hypothesis, but the null is actually false.

Ex. Education has an effect on wage, but we incorrectly fail to reject \(H_0\).

This is an error. Defined as a Type II error.

Possible outcomes

Within this structure, four possible outcomes exist:

1. We fail to reject the null hypothesis and the null is true.

2. We reject the null hypothesis and the null is false.

3. We reject the null hypothesis, but the null is actually true.¹

4. We fail to reject the null hypothesis, but the null is actually false.²

1. Type I error

2. Type II error

Or… from the golden age of textbook illustrations

How I think of it

Hypothesis Tests

Goal: Make a statement about \(\beta_1\) using information on \(\hat{\beta}_1\).

\(\hat{\beta}_1\) is random—it could be anything, even if \(\beta_1 = 0\) is true.

• But if \(\beta_1 = 0\) is true, then \(\hat{\beta}_1\) is unlikely to take values far from zero.
• As the standard error shrinks, we are even less likely to observe “extreme” values of \(\hat{\beta}_1\) (assuming \(\beta_1 = 0\)).

Hypothesis testing takes extreme values of \(\hat{\beta}_1\) as evidence against the null hypothesis, but it will weight them by information about variance the estimated variance of \(\hat{\beta}_1\).

Hypothesis Tests

\(H_0\): \(\beta_1 = 0\)

\(H_1\): \(\beta \neq 0\)

To conduct the test, we calculate a \(t\)-statistic¹:

\[ t = \frac{\hat{\beta}_1 - \beta_1^0}{\mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right)} \]

Distributed by a \(t\)-distribution with \(n-2\) degrees of freedom².

1. \(\beta_1^0\) is the value of \(\beta_1\) in our null hypothesis (e.g., \(\beta_1^0 = 0\)).

2. represents the number of independent values in a sample that are free to vary when estimating statistical parameters.

Hypothesis Testing

Normal distribution vs. \(t\) distribution

• A normal distribution has the same shape for any sample size.
• The shape of the t distribution depends the degrees of freedom.

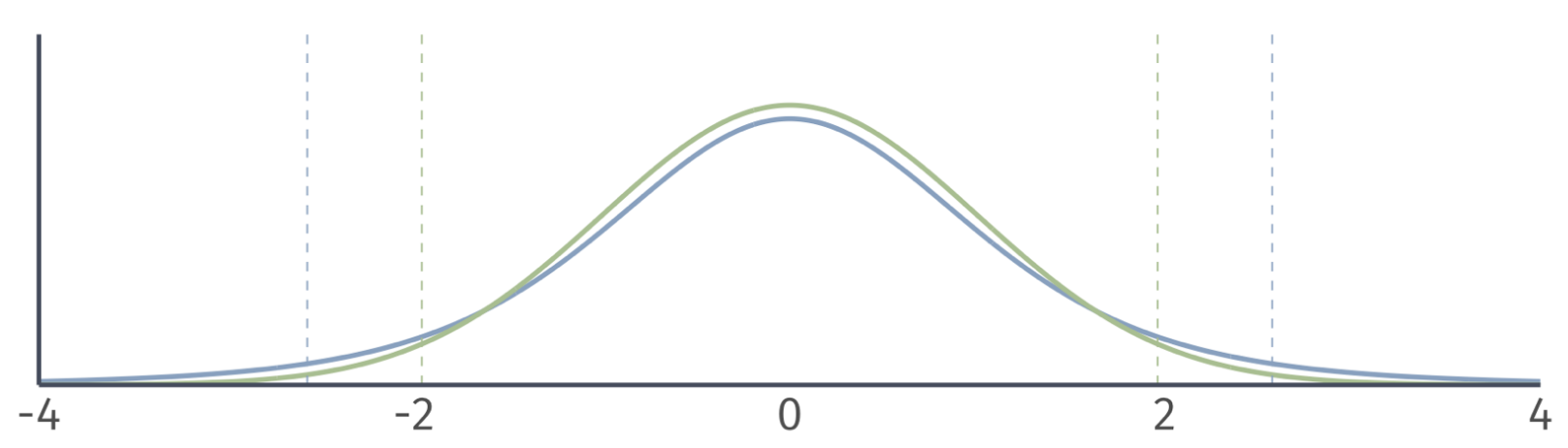
• Degrees of freedom = 5.

Hypothesis Testing

Normal distribution vs. \(t\) distribution

• A normal distribution has the same shape for any sample size.
• The shape of the t distribution depends the degrees of freedom.

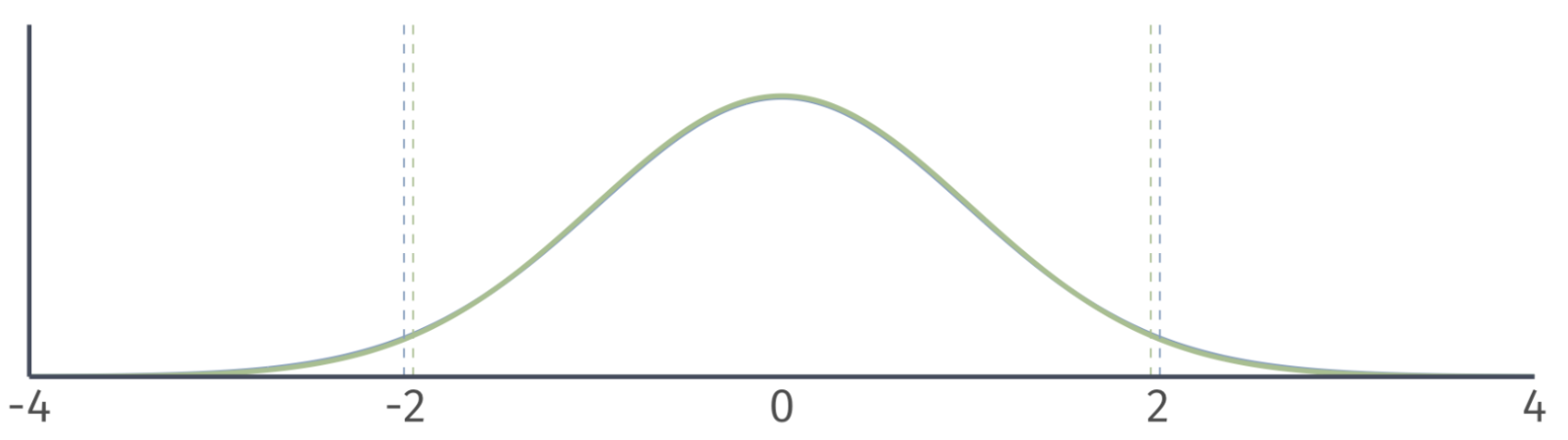
• Degrees of freedom = 50.

Hypothesis Testing

Normal distribution vs. \(t\) distribution

• A normal distribution has the same shape for any sample size.
• The shape of the t distribution depends the degrees of freedom.

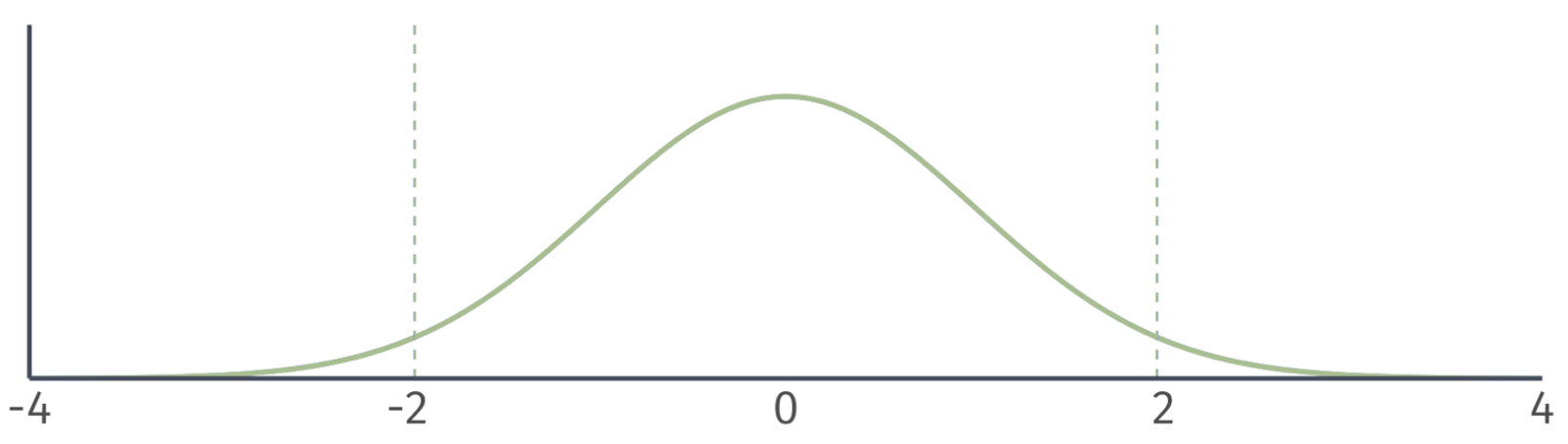
• Degrees of freedom = 500.

Hypothesis Testing

Two sided t Tests

To conduct a t test, compare the \(t\) statistic to the appropriate critical value of the t distribution.

• To find the critical value in a t table, we need the degrees of freedom and the significance level \(\alpha\).

Reject (\(\text{H}_0\)) at the \(\alpha \cdot 100\)-percent level if

\[ \left| t \right| = \left| \dfrac{\hat{\mu} - \mu_0}{\mathop{\text{SE}}(\hat{\mu})} \right| > t_\text{crit}. \]

Hypothesis Tests

Next, we use the \(\color{#434C5E}{t}\)-statistic to calculate a \(\color{#B48EAD}{p}\)-value.

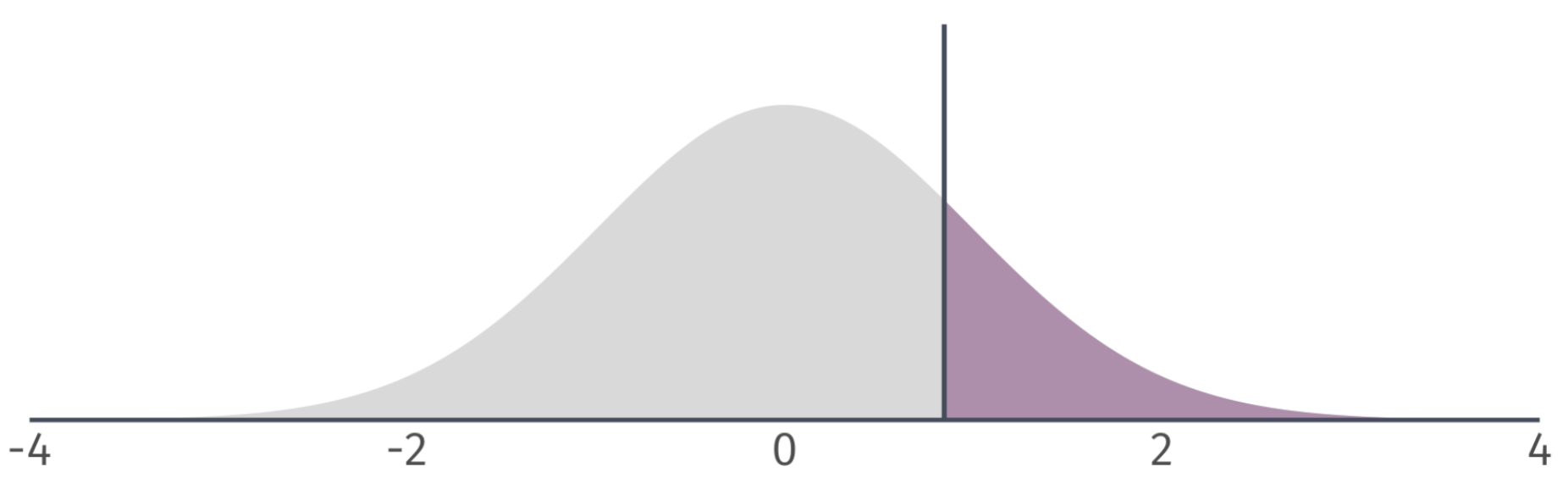
Describes the probability of seeing a \(\color{#434C5E}{t}\)-statistic as extreme as the one we observe if the null hypothesis is actually true.

But…we still need some benchmark to compare our \(\color{#B48EAD}{p}\)-value against.

Hypothesis Tests

We worry mostly about false positives, so we conduct hypothesis tests based on the probability of making a Type I error¹.

How? We select a significance level, \(\color{#434C5E}{\alpha}\), that specifies our tolerance for false positives (i.e., the probability of Type I error we choose to live with).

1. We reject the null hypothesis, but the null is actually true.

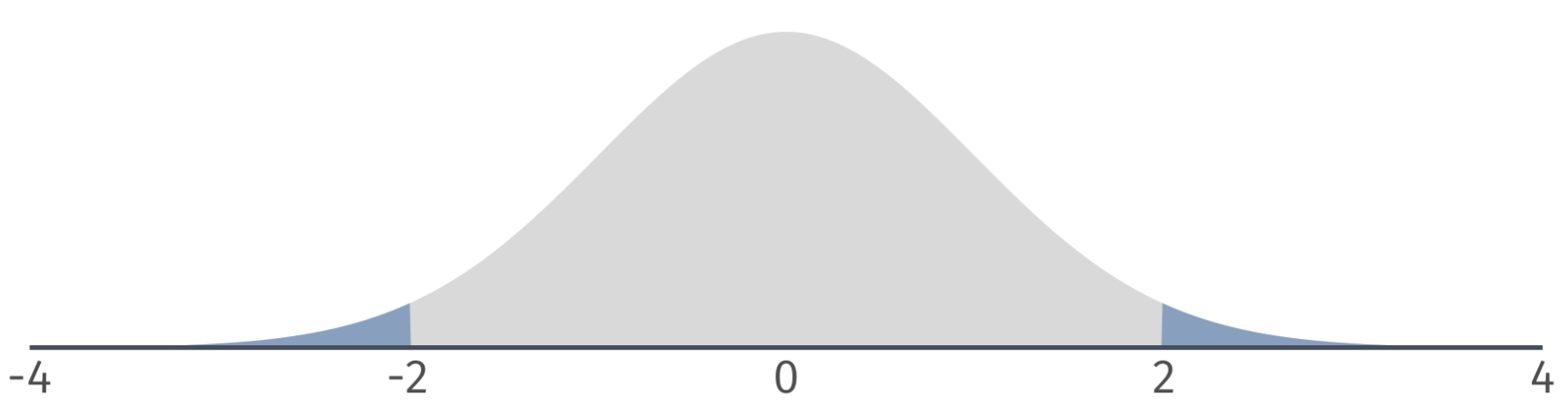
To visualize Type I and Type II, we can plot the sampling distributions of \(\hat{\beta}_1\) under the null and alternative hypotheses

Hypothesis Tests

We then compare \(\color{#434C5E}{\alpha}\) to the \(\color{#B48EAD}{p}\)-value of our test.

• If the \(\color{#B48EAD}{p}\)-value is less than \(\color{#434C5E}{\alpha}\), then we reject the null hypothesis at the \(\color{#434C5E}{\alpha}\cdot100\) percent level.

• If the \(\color{#B48EAD}{p}\)-value is greater than \(\color{#434C5E}{\alpha}\), then we fail to reject the null hypothesis at the \(\color{#434C5E}{\alpha}\cdot100\) percent level.¹

1. Note: Fail to reject \(\neq\) accept.

Ex. Are campus police associated with campus crime?

\(H_0\): \(\beta_\text{Police} = 0\)
\(H_1\): \(\beta_\text{Police} \neq 0\)

Significance level: \(\color{#434C5E}{\alpha} = 0.05\) (i.e., 5 percent test)

Test Condition: Reject \(H_0\) if \(p < \alpha\)

What is the \(\color{#B48EAD}{p}\)-value? \(p = 0.18\)

Do we reject the null hypothesis? No.

Hypothesis Tests

\(\color{#B48EAD}{p}\)-values are difficult to calculate by hand.

Alternative: Compare \(\color{#434C5E}{t}\)-statistic to critical values from the \({\color{#434C5E} t}\)-distribution.

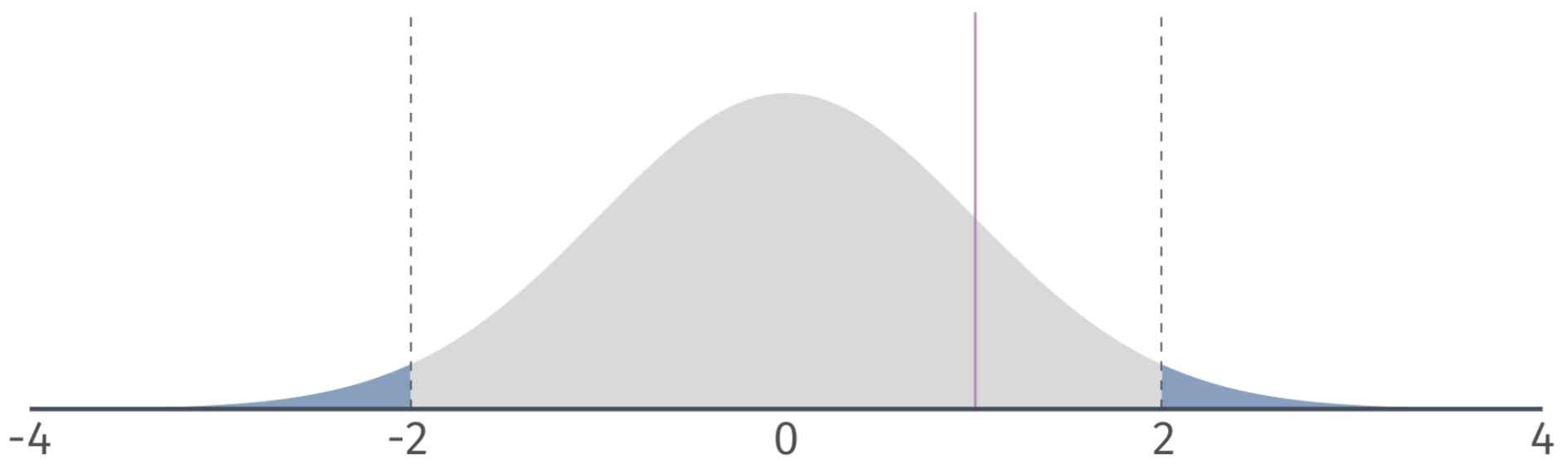
Hypothesis Tests

Notation: \(t_{1-\alpha/2, n-2}\) or \(t_\text{crit}\).

• Find in a \(t\)-table using \(\color{#434C5E}{\alpha}\) and \(n-2\) degrees of freedom.

Compare the the critical value to your \(t\)-statistic:

• If \(|t| > |t_{1-\alpha/2, n-2}|\), then reject the null.
• If \(|t| < |t_{1-\alpha/2, n-2}|\), then fail to reject the null.

Two-sided tests

Based on a critical value of \(t_{1-\alpha/2, n-2} = t_{0.975, 100} = 1.98\) we can identify a rejection region on the \(\color{#434C5E}{t}\)-distribution.

If our \(\color{#434C5E}{t}\)-statistic is in the rejection region, then we reject the null hypothesis at the 5 percent level.

Ex.¹ \(\alpha = 0.05\)

\(H_0\): \(\beta_1 = 0\)
\(H_1\): \(\beta_1 \neq 0\)

Notice that the \(\color{#434C5E}{t}\)-statistic is 7.15. The critical value is \(\color{#434C5E}{t_{\text{0.975, 28}}} = 2.05\).

Which implies that \(p < 0.05\). Therefore, we reject \(H_0\) at the 5% level.

1. {{< fa brands r-project >}} defaults to testing hypotheses against the null hypothesis of zero.

Ex. Are campus police associated with campus crime? (\(\alpha = 0.1\))

\(H_0\): \(\beta_\text{Police} = 0\)
\(H_1\): \(\beta_\text{Police} \neq 0\)

The \(\color{#434C5E}{t \text{-stat}} = 1.35\). The critical value is \(\color{#434C5E}{t_{\text{0.95, 94}}} = 1.66\).

|\(\color{#434C5E}{t \text{-stat}}| < |\color{#434C5E}{t_{\text{crit}}}|\) implies that \(p > 0.05\). Therefore, we fail to reject \(H_0\) at the 10% level.

One-sided tests

We might be confident in a parameter being non-negative/non-positive.

One-sided tests assume that the parameter of interest is either greater than/less than \(H_0\).

• Option 1 \(H_0\): \(\beta_1 = 0\) vs. \(H_1\): \(\beta_1 > 0\)

• Option 2 \(H_0\): \(\beta_1 = 0\) vs. \(H_1\): \(\beta_1 < 0\)

If this assumption is reasonable, then our rejection region changes.

• Same \(\alpha\).

One-sided tests

Left-tailed: Based on a critical value of \(t_{1-\alpha, n-2} = t_{0.95, 100} = 1.66\), we can identify a rejection region on the \(t\)-distribution.

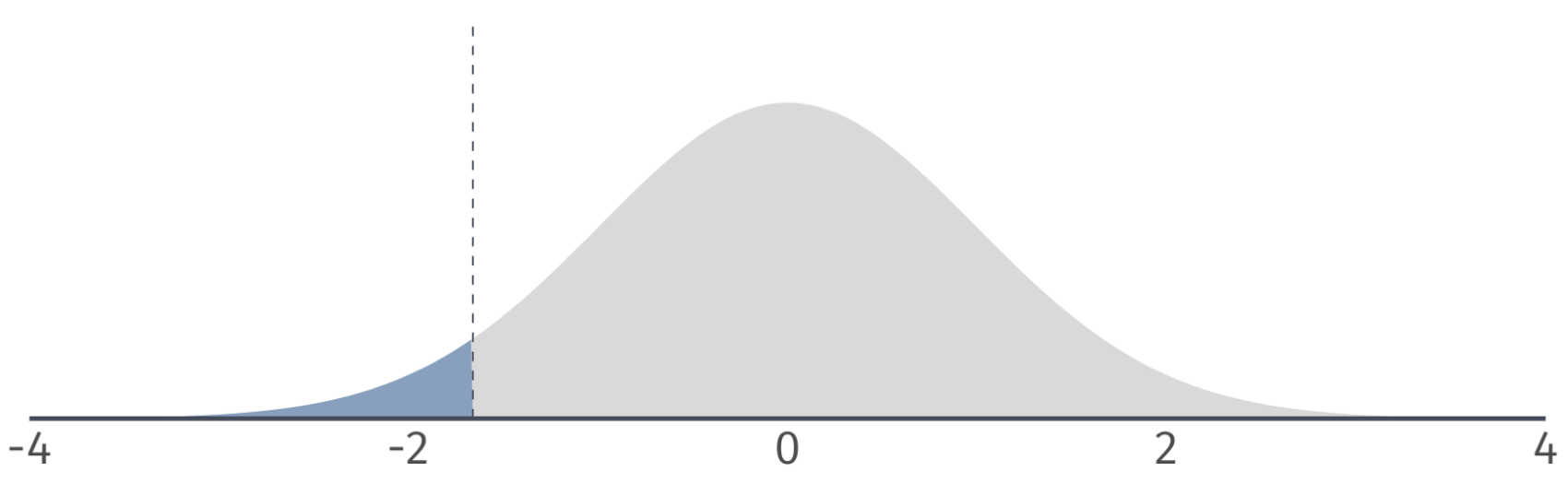
If our \(t\) statistic is in the rejection region, then we reject the null hypothesis at the 5 percent level.

One-sided tests

Right-tailed: Based on a critical value of \(t_{1-\alpha, n-2} = t_{0.95, 100} = 1.66\), we can identify a rejection region on the \(t\)-distribution.

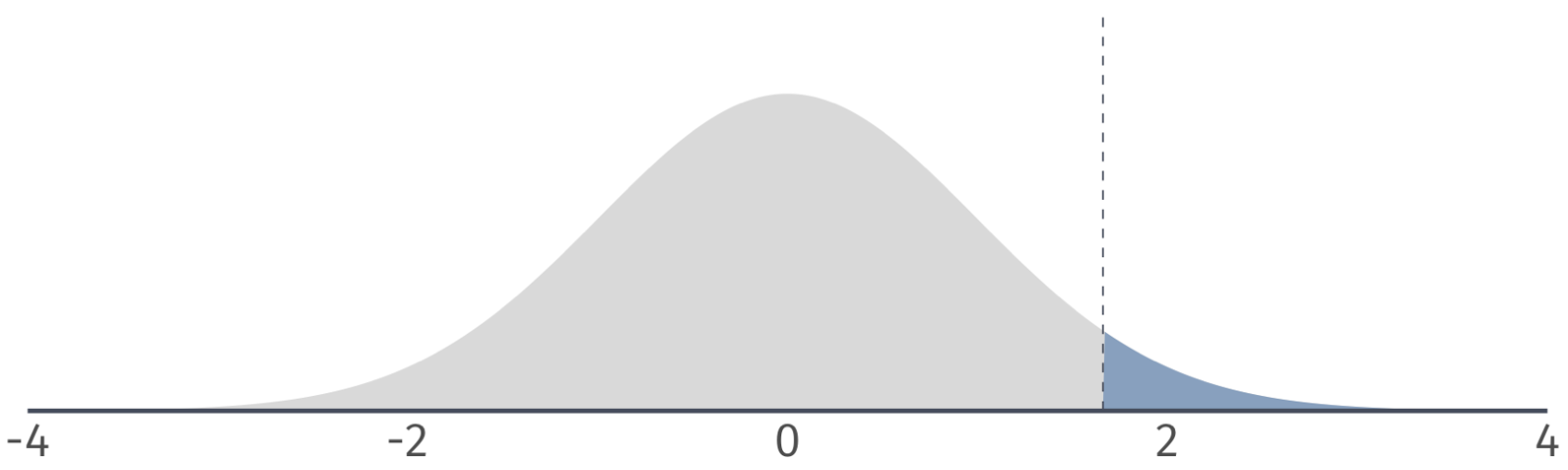
If our \(t\) statistic is in the rejection region, then we reject the null hypothesis at the 5 percent level.

Ex. Do campus police deter campus crime? (\(\alpha = 0.1\))

Suppose we rule out the possibility that police increase crime, but not that they have no effect.

\(H_0\): \(\beta_\text{Police} = 0\)
\(H_1\): \(\beta_\text{Police} < 0\)

Notice that the \(\color{#434C5E}{t \text{-stat}} = 1.35\). The critical value is \(\color{#434C5E}{t_{\text{0.9, 94}}} = 1.29\).

Which implies that \(p > 0.05\). Therefore, we reject \(H_0\) at the 5% level.

Confidence Intervals

Confidence intervals

Until now, we have considered point estimates of population parameters.

• Sometimes a range of values is more interesting/honest.

We can construct \((1-\alpha)\cdot100\)-percent level confidence intervals for \(\beta_1\)

\[ \hat{\beta}_1 \pm t_{1-\alpha/2, n-2} \, \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \]

\(t_{1-\alpha/2,n-2}\) denotes the \(1-\alpha/2\) quantile of a \(t\) distribution with \(n-2\) degrees of freedom.

Confidence intervals

Q: Where does the confidence interval formula come from?

A: Formula is a result from the rejection condition of a two-sided test.

Reject \(H_0\) if

\[ |t| > t_\text{crit} \]

The test condition implies that we:

Fail to reject \(H_0\) if

\[ |t| \leq t_\text{crit} \]

or, \[ -t_\text{crit} \leq t \leq t_\text{crit} \]

Confidence intervals

Replacing \(t\) with its formula gives:

Fail to reject \(H_0\) if

\[-t_\text{crit} \leq \frac{\hat{\beta}_1 - \beta_1^0}{\mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right)} \leq t_\text{crit} \]

Standard errors are always positive, so the inequalities do not flip when we multiply by \(\mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right)\):

Fail to reject \(H_0\) if \[ -t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \leq \hat{\beta}_1 - \beta_1^0\leq t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \]

Confidence intervals

Subtracting \(\hat{\beta}_1\) yields

Fail to reject \(H_0\) if \[ -\hat{\beta}_1 -t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \leq - \beta_1^0 \leq - \hat{\beta}_1 + t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \]

Multiplying by -1 and rearranging gives

Fail to reject \(H_0\) if

\[ \hat{\beta}_1 - t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \leq \beta_1^0 \leq \hat{\beta}_1 + t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \]

Confidence intervals

Replacing \(\beta_1^0\) with \(\beta_1\) and dropping the test condition yields the interval:

\[ \hat{\beta}_1 - t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \leq \beta_1 \leq \hat{\beta}_1 + t_\text{crit} \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \]

which is equivalent to

\[ \hat{\beta}_1 \pm t_\text{crit} \, \mathop{\hat{\text{SE}}} \left( \hat{\beta}_1 \right) \]

Confidence intervals

Main insight:

• If a 95 percent confidence interval contains zero, then we fail to reject the null hypothesis at the 5 percent level.
• If a 95 percent confidence interval does not contain zero, then we reject the null hypothesis at the 5 percent level.

Generally, a \((1- \alpha) \cdot 100\) percent confidence interval embeds a two-sided test at the \(\alpha \cdot 100\) level.

Confidence intervals Ex.

95% confidence interval for \(\beta_1\) is:

\[ 0.567 \pm 1.98 \times 0.0793 = \left[ 0.410,\, 0.724 \right] \]

Confidence intervals

We have a confidence interval for \(\beta_1\), i.e., \(\left[ 0.410,\, 0.724 \right]\)

What does it mean?

Informally: The confidence interval gives us a region (interval) in which we can place some trust (confidence) for containing the parameter.

More formally: If we repeatedly sample from our population and construct confidence intervals for each of these samples, then \((1-\alpha) \cdot100\) percent of our intervals (e.g., 95%) will contain the population parameter somewhere in the interval.

Confidence intervals

Going back to our simulation…

We drew 10,000 samples (each of size \(n = 30\)) from our population and estimated our regression model for each sample:

\[ Y_i = \hat{\beta}_1 + \hat{\beta}_1 X_i + \hat{u}_i \]

(repeated 10,000 times)

The true parameter values are \(\beta_0 = 0\) and \(\beta_1 = 0.5\)

Let’s estimate 95% confidence intervals for each of these intervals…

Confidence intervals

From our previous simulation, 97.7% of 95% confidence intervals contain the true parameter value of \(\beta_1\).

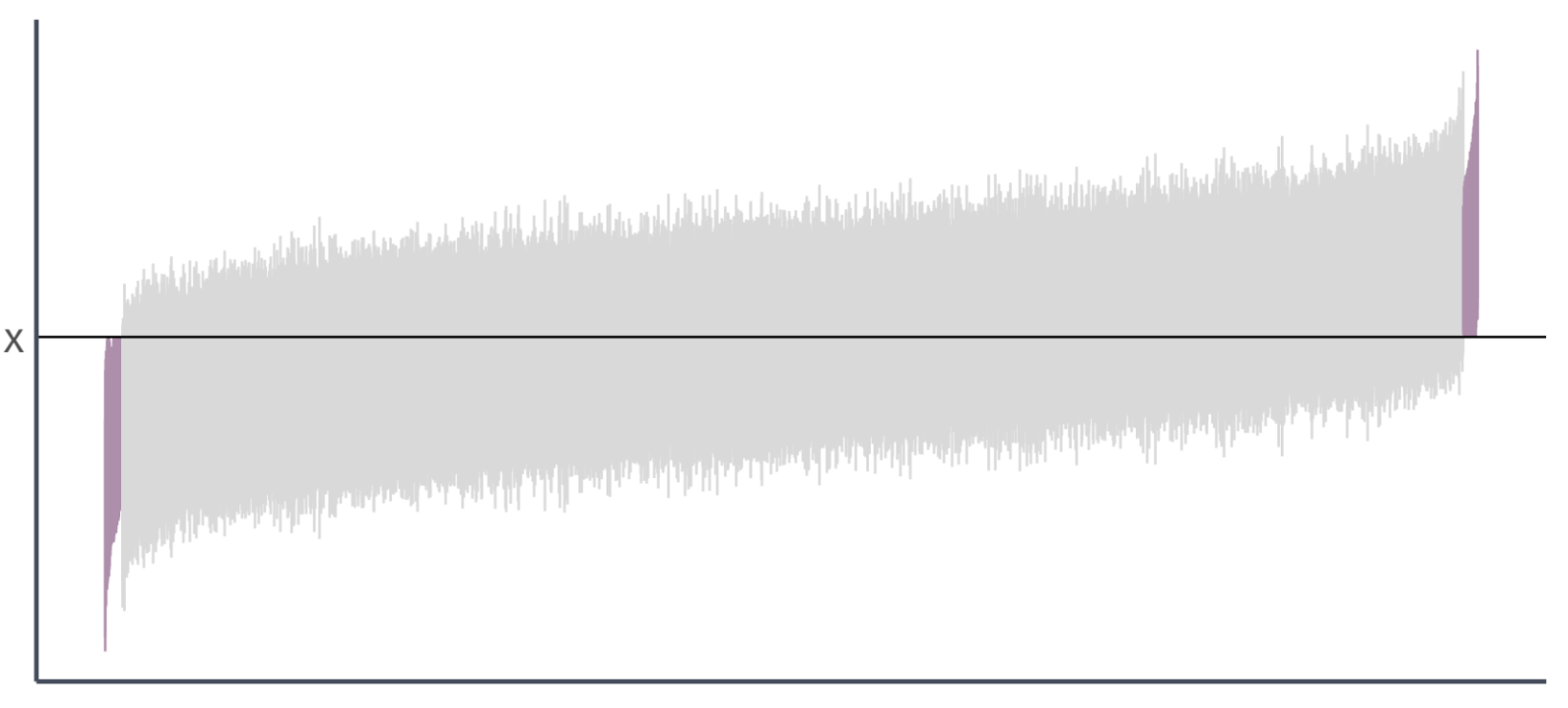
Ex. Association of police with crime

You can instruct tidy to return a 95 percent confidence interval for the association of campus police with campus crime:

Ex. Association of police with crime

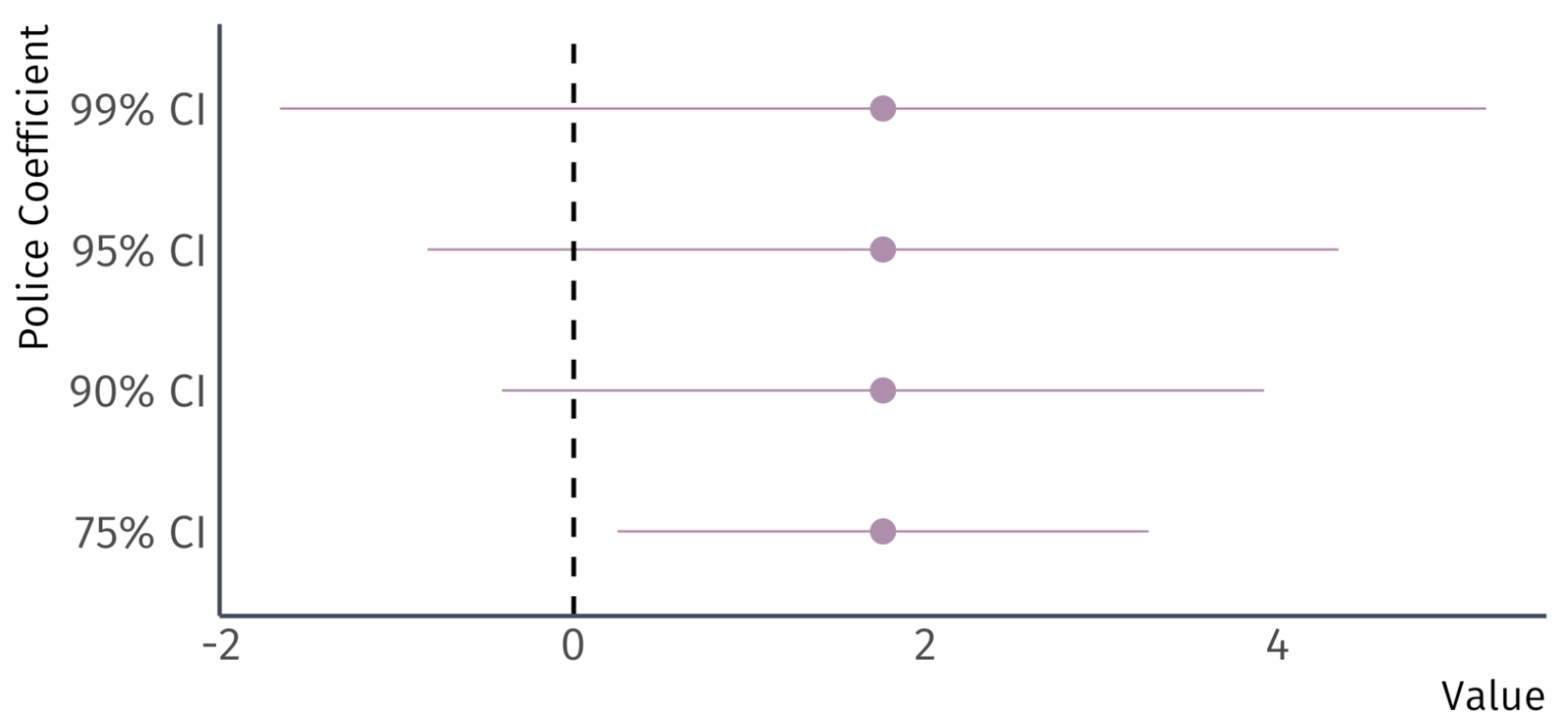
Four confidence intervals for the same coefficient.