Categorical Variables and Interactions
EC 320 - Introduction to Econometrics
2025
Categorical Variables
Categorical Variables
Goal Make quantitative statements about qualitative information.
- e.g., race, gender, being employed, living in Oregon, etc.
Approach. Construct binary variables.
- a.k.a. dummy variables or indicator variables.
- Value equals 1 if observation is in the category or 0 if otherwise.
Regression implications.
Change the interpretation of the intercept.
Change the interpretations of the slope parameters.
Continuous Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + u_i \]
where
- \(\text{Pay}_i\) is a continuous variable measuring an individual’s pay
- \(\text{School}_i\) is a continuous variable that measures years of education
Interpretation
- \(\beta_0\): \(y\)-intercept, i.e., \(\text{Pay}\) when \(\text{School} = 0\)
- \(\beta_1\): expected increase in \(\text{Pay}\) for a one-unit increase in \(\text{School}\)
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + u_i \]
Derive the slope’s interpretation.
\(\mathop{\mathbb{E}}\left[ \text{Pay} | \text{School} = \ell + 1 \right] - \mathop{\mathbb{E}}\left[ \text{Pay} | \text{School} = \ell \right]\)
\(\quad = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1 (\ell + 1) + u \right] - \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1 \ell + u \right]\)
\(\quad = \left[ \beta_0 + \beta_1 (\ell + 1) \right] - \left[ \beta_0 + \beta_1 \ell \right]\)
\(\quad = \beta_0 - \beta_0 + \beta_1 \ell - \beta_1 \ell + \beta_1\) \(\: = \beta_1\).
Expected increase in pay for an additional year of schooling
Continuous Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + u_i \]
Alternative derivation:
Differentiate the model with respect to schooling:
\[ \dfrac{\partial \text{Pay}}{\partial \text{School}} = \beta_1 \]
Expected increase in pay for an additional year of schooling
If we have multiple explanatory variables, e.g.,
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + \beta_2 \text{Ability}_i + u_i \]
then the interpretation changes slightly.
\(\mathop{\mathbb{E}}\left[ \text{Pay} | \text{School} = \ell + 1 \land \text{Ability} = \alpha \right] - \mathop{\mathbb{E}}\left[ \text{Pay} | \text{School} = \ell \land \text{Ability} = \alpha \right]\)
\(\quad = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1 (\ell + 1) + \beta_2 \alpha + u \right] - \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1 \ell + \beta_2 \alpha + u \right]\)
\(\quad = \left[ \beta_0 + \beta_1 (\ell + 1) + \beta_2 \alpha \right] - \left[ \beta_0 + \beta_1 \ell + \beta_2 \alpha \right]\)
\(\quad = \beta_0 - \beta_0 + \beta_1 \ell - \beta_1 \ell + \beta_1 + \beta_2 \alpha - \beta_2 \alpha\) \(\: = \beta_1\)
The slope gives the expected increase in pay for an additional year of schooling, holding ability constant.
Continuous Variables
If we have multiple explanatory variables, e.g.,
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + \beta_2 \text{Ability}_i + u_i \]
then the interpretation changes slightly.
Alternative derivation
Differentiate the model with respect to schooling:
\[ \dfrac{\partial\text{Pay}}{\partial\text{School}} = \beta_1 \]
The slope gives the expected increase in pay for an additional year of schooling, holding ability constant.
Categorical Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{Female}_i + u_i \]
where \(\text{Pay}_i\) is a continuous variable measuring an individual’s pay and \(\text{Female}_i\) is a binary variable equal to \(1\) when \(i\) is female.
Interpretation of \(\beta_0\)
\(\beta_0\) is the expected \(\text{Pay}\) for males (i.e., when \(\text{Female} = 0\)):
\[ \mathop{\mathbb{E}}\left[ \text{Pay} | \text{Male} \right] = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1\times 0 + u_i \right] = \mathop{\mathbb{E}}\left[ \beta_0 + 0 + u_i \right] = \beta_0 \]
Categorical Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{Female}_i + u_i \]
where \(\text{Pay}_i\) is a continuous variable measuring an individual’s pay and \(\text{Female}_i\) is a binary variable equal to \(1\) when \(i\) is female.
Interpretation of \(\beta_1\)
\(\beta_1\) is the expected difference in \(\text{Pay}\) between females and males:
\(\mathop{\mathbb{E}}\left[ \text{Pay} | \text{Female} \right] - \mathop{\mathbb{E}}\left[ \text{Pay} | \text{Male} \right]\)
\(\quad = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1\times 1 + u_i \right] - \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1\times 0 + u_i \right]\)
\(\quad = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1 + u_i \right] - \mathop{\mathbb{E}}\left[ \beta_0 + 0 + u_i \right]\)
\(\quad = \beta_0 + \beta_1 - \beta_0\) \(\quad = \beta_1\)
Categorical Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{Female}_i + u_i \]
where \(\text{Pay}_i\) is a continuous variable measuring an individual’s pay and \(\text{Female}_i\) is a binary variable equal to \(1\) when \(i\) is female.
Interpretation
\(\beta_0 + \beta_1\): is the expected \(\text{Pay}\) for females:
\(\mathop{\mathbb{E}}\left[ \text{Pay} | \text{Female} \right]\)
\(\quad = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1\times 1 + u_i \right]\)
\(\quad = \mathop{\mathbb{E}}\left[ \beta_0 + \beta_1 + u_i \right]\)
\(\quad = \beta_0 + \beta_1\)
Categorical Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{Female}_i + u_i \]
Interpretation
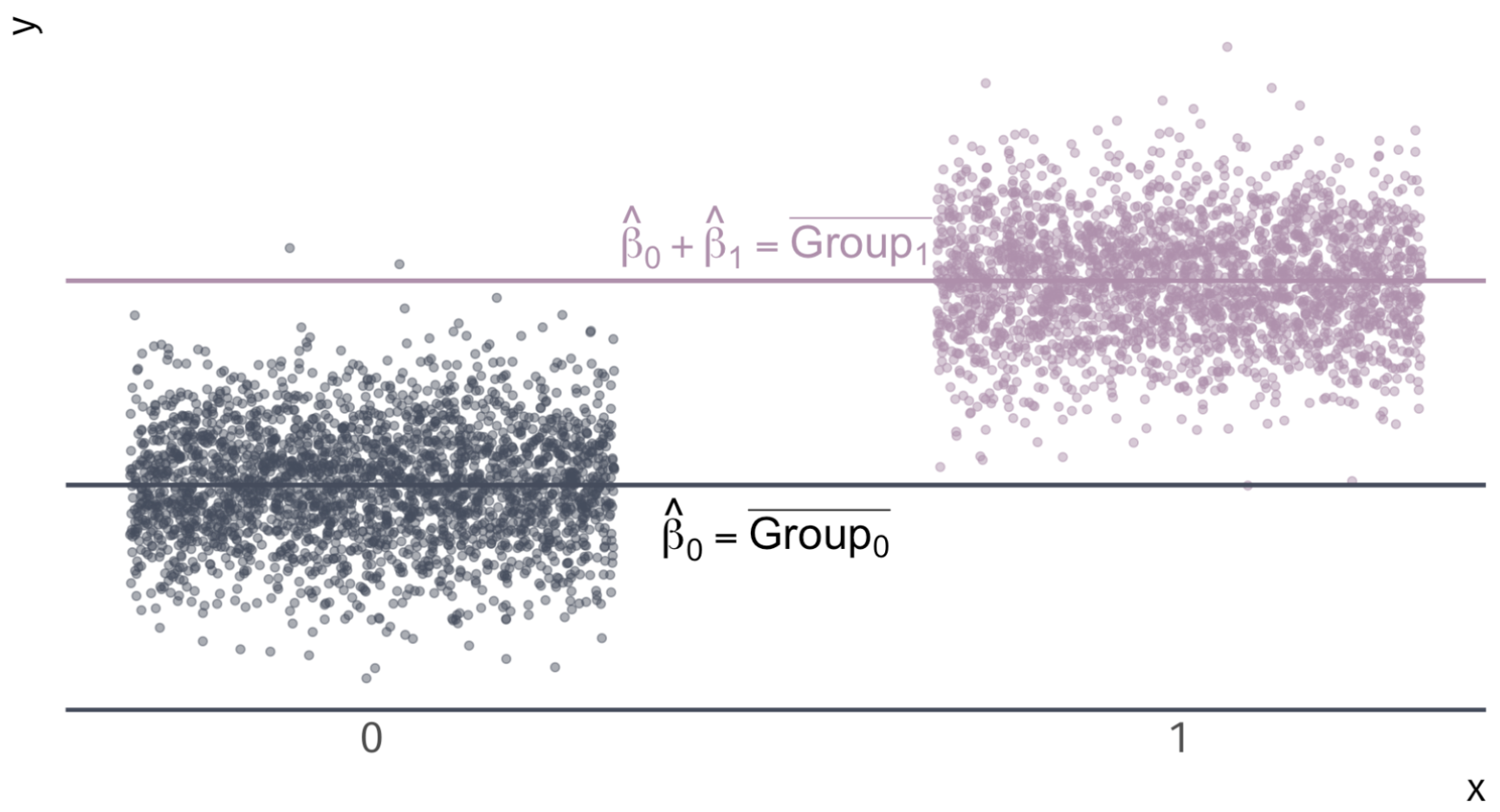
- \(\beta_0\): expected \(\text{Pay}\) for males (i.e., when \(\text{Female} = 0\))
- \(\beta_1\): expected difference in \(\text{Pay}\) between females and males
- \(\beta_0 + \beta_1\): expected \(\text{Pay}\) for females
- Males are the reference group
Categorical Variables
Consider the relationship
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{Female}_i + u_i \]
Note. If there are no other variables to condition on, then \(\hat{\beta}_1\) equals the difference in group means, e.g., \(\bar{X}_\text{Female} - \bar{X}_\text{Male}\).
Note2. The holding all other variables constant interpretation also applies for categorical variables in multiple regression settings.
Categorical Variables
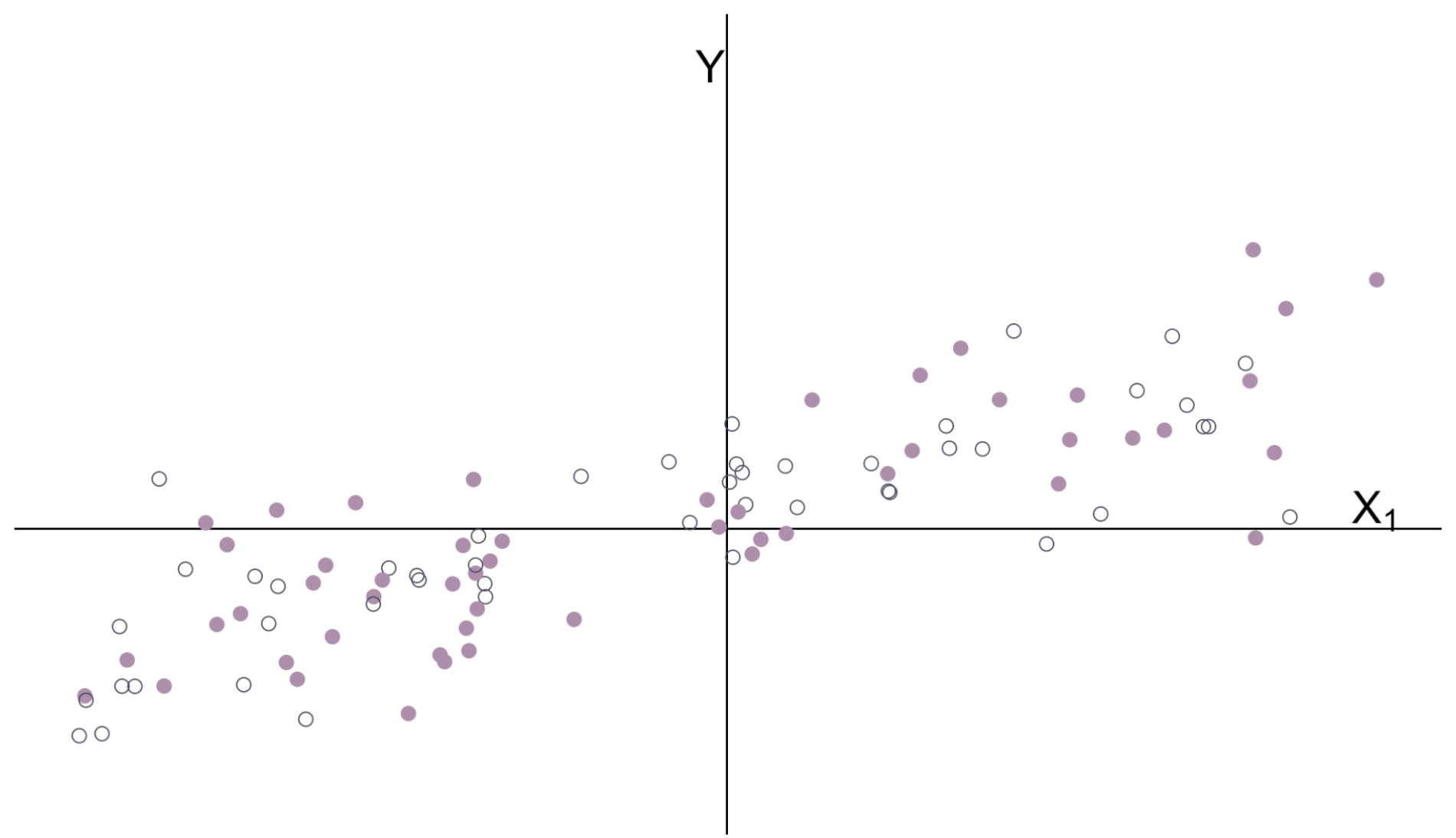
\(Y_i = \beta_0 + \beta_1 X_i + u_i\) for binary variable \(X_i = \{\color{#434C5E}{0}, \, {\color{#B48EAD}{1}}\}\)

Categorical Variables
\(Y_i = \beta_0 + \beta_1 X_i + u_i\) for binary variable \(X_i = \{\color{#434C5E}{0}, \, {\color{#B48EAD}{1}}\}\)
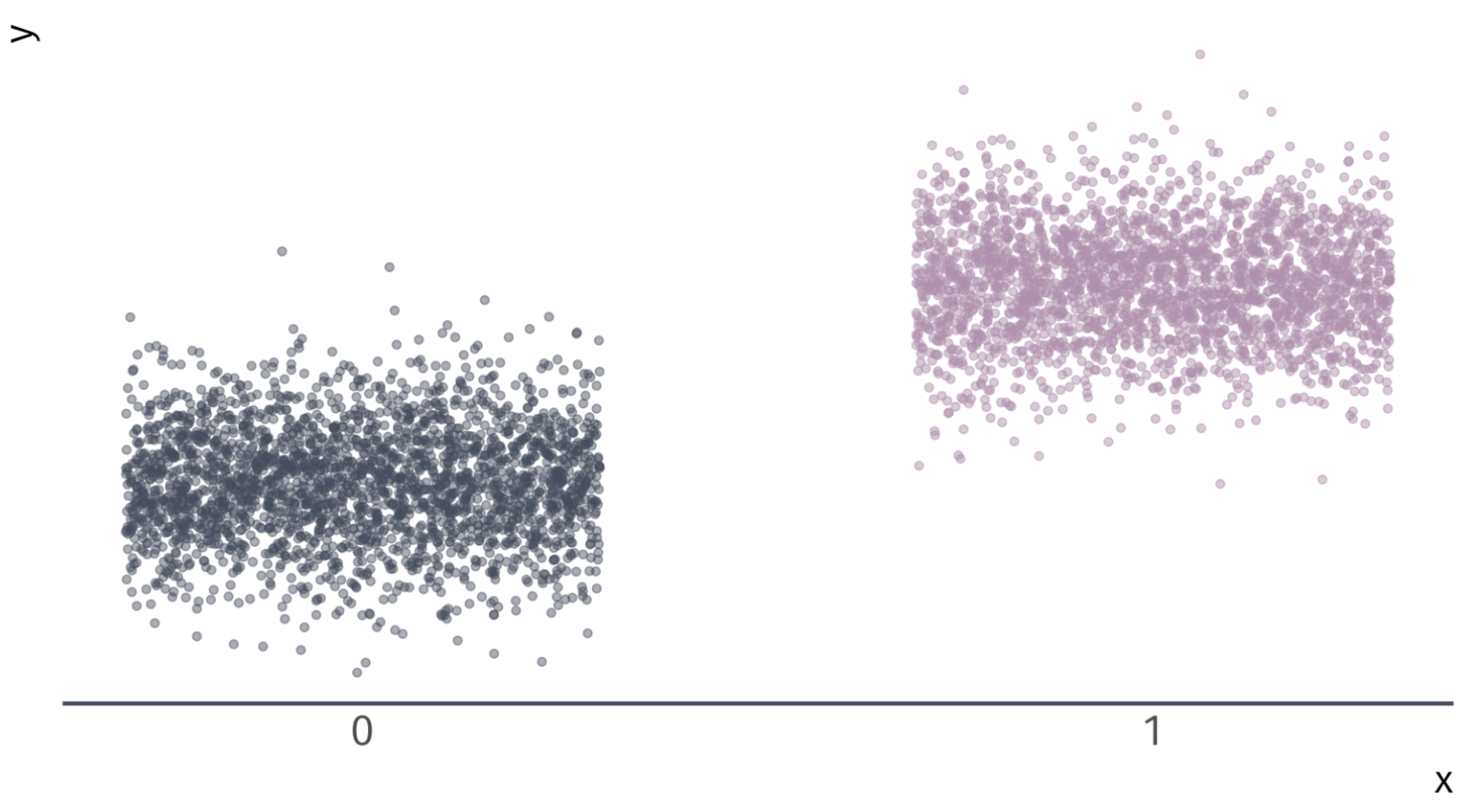
Categorical Variables
\(Y_i = \beta_0 + \beta_1 X_i + u_i\) for binary variable \(X_i = \{\color{#434C5E}{0}, \, {\color{#B48EAD}{1}}\}\)
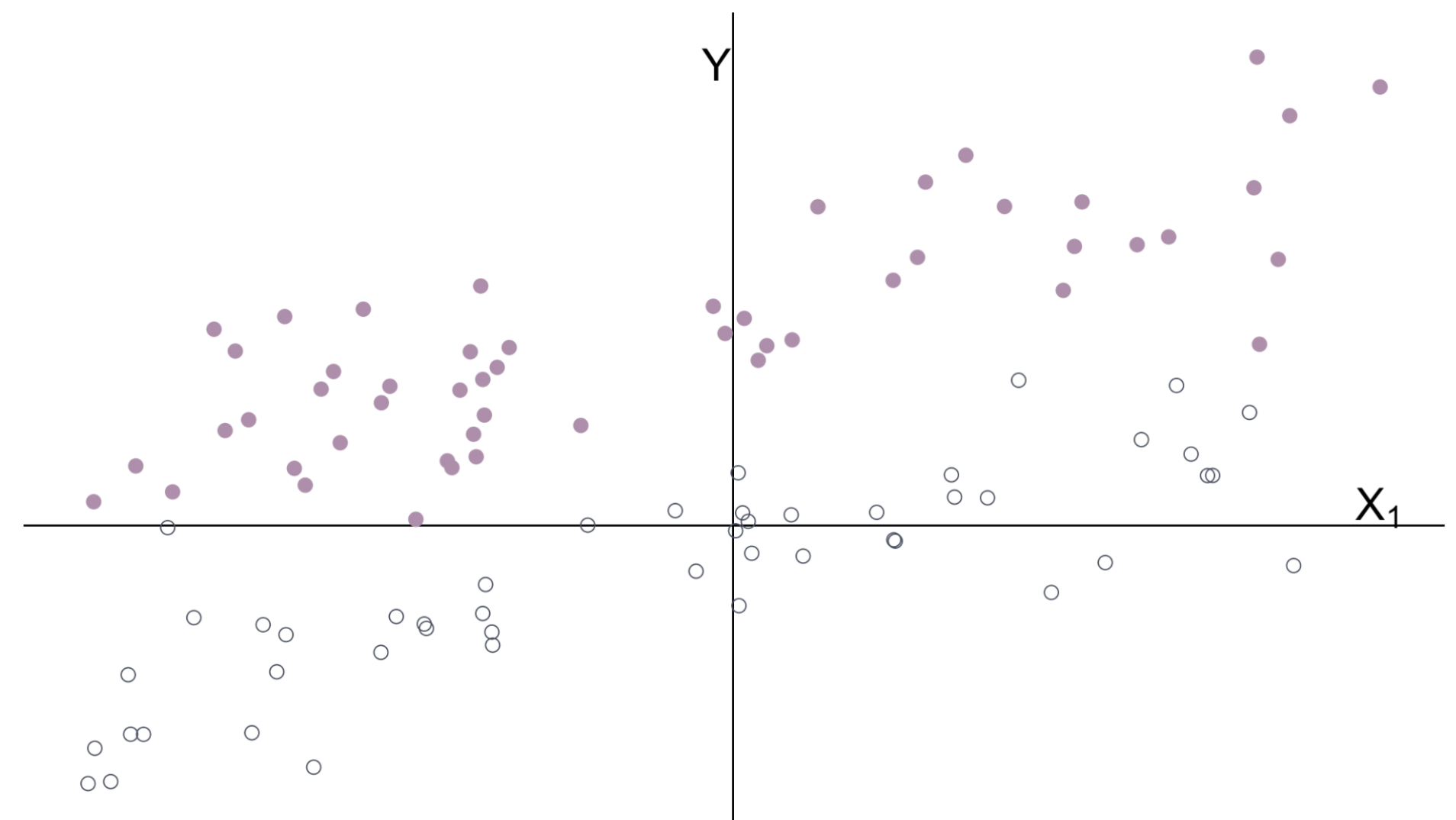
Multiple Regression
\(Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + u_i \quad\) \(X_1\) is continuous \(\quad X_2\) is categorical
Multiple Regression
The intercept and categorical variable \(X_2\) control for the groups’ means.
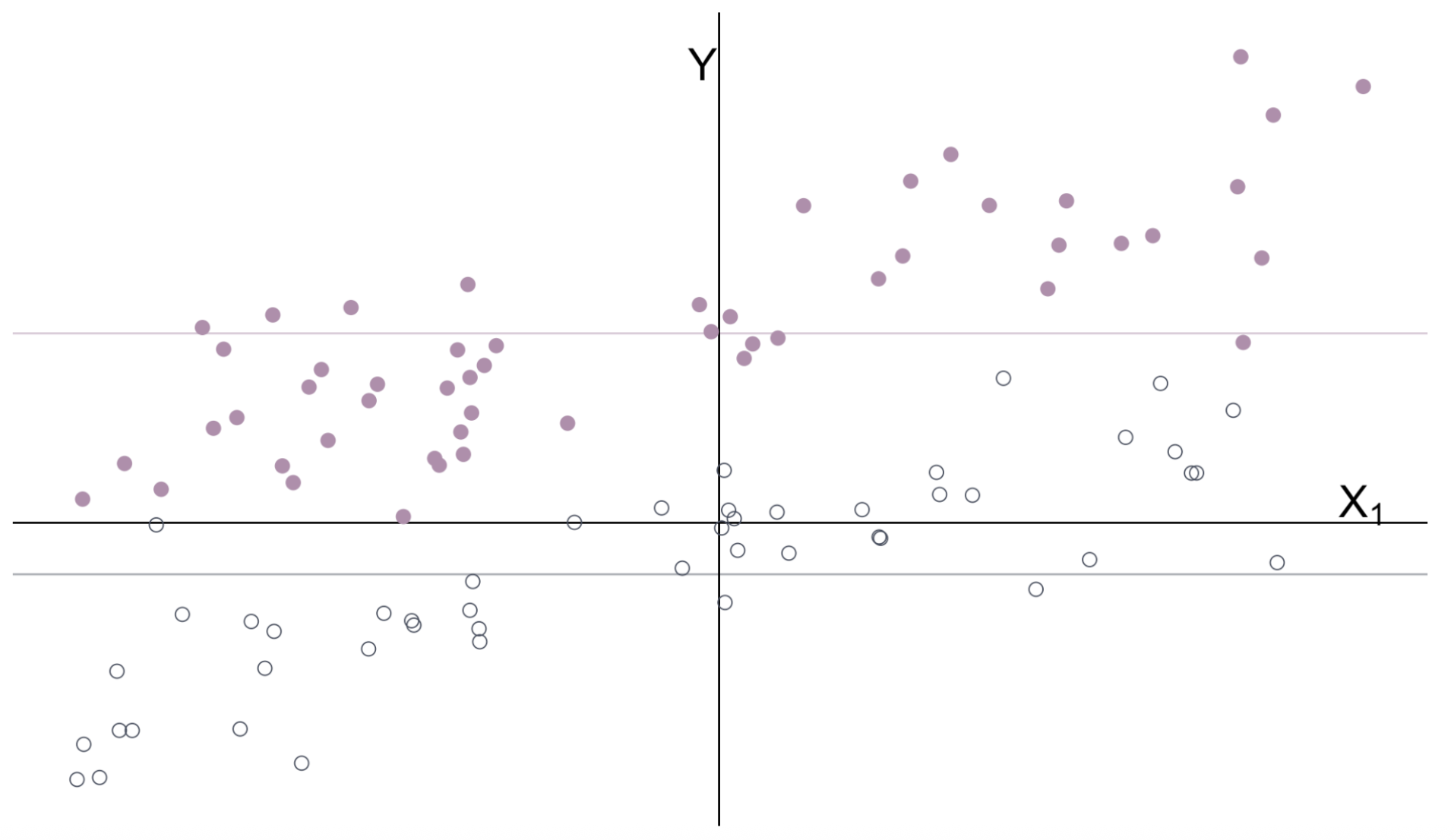
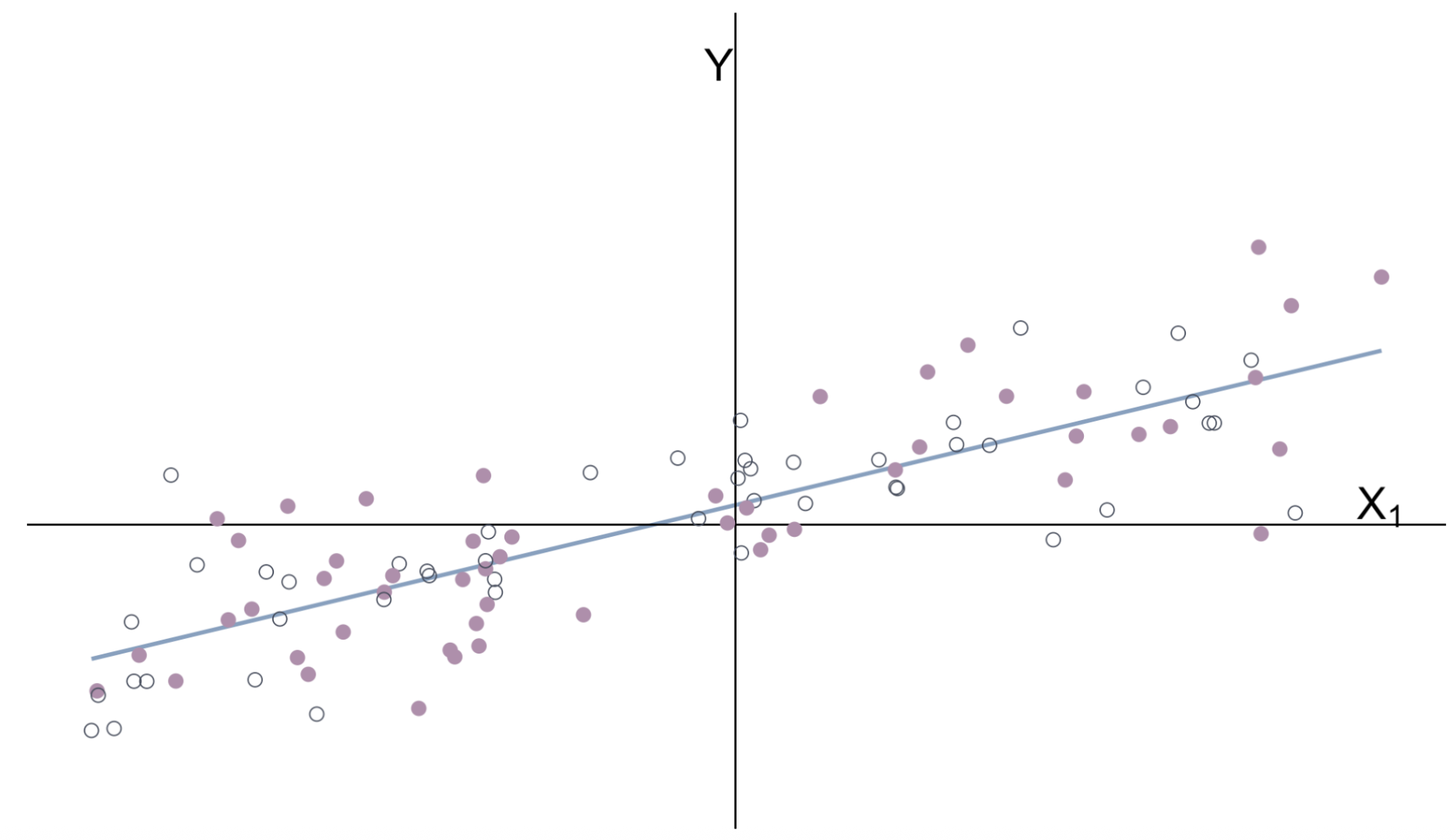
Multiple Regression
With groups’ means removed
Multiple Regression
\(\hat{\beta}_1\) estimates the relationship between \(Y\) and \(X_1\) after controlling for \(X_2\).
Multiple Regression
Another way to think about it: Regression by group
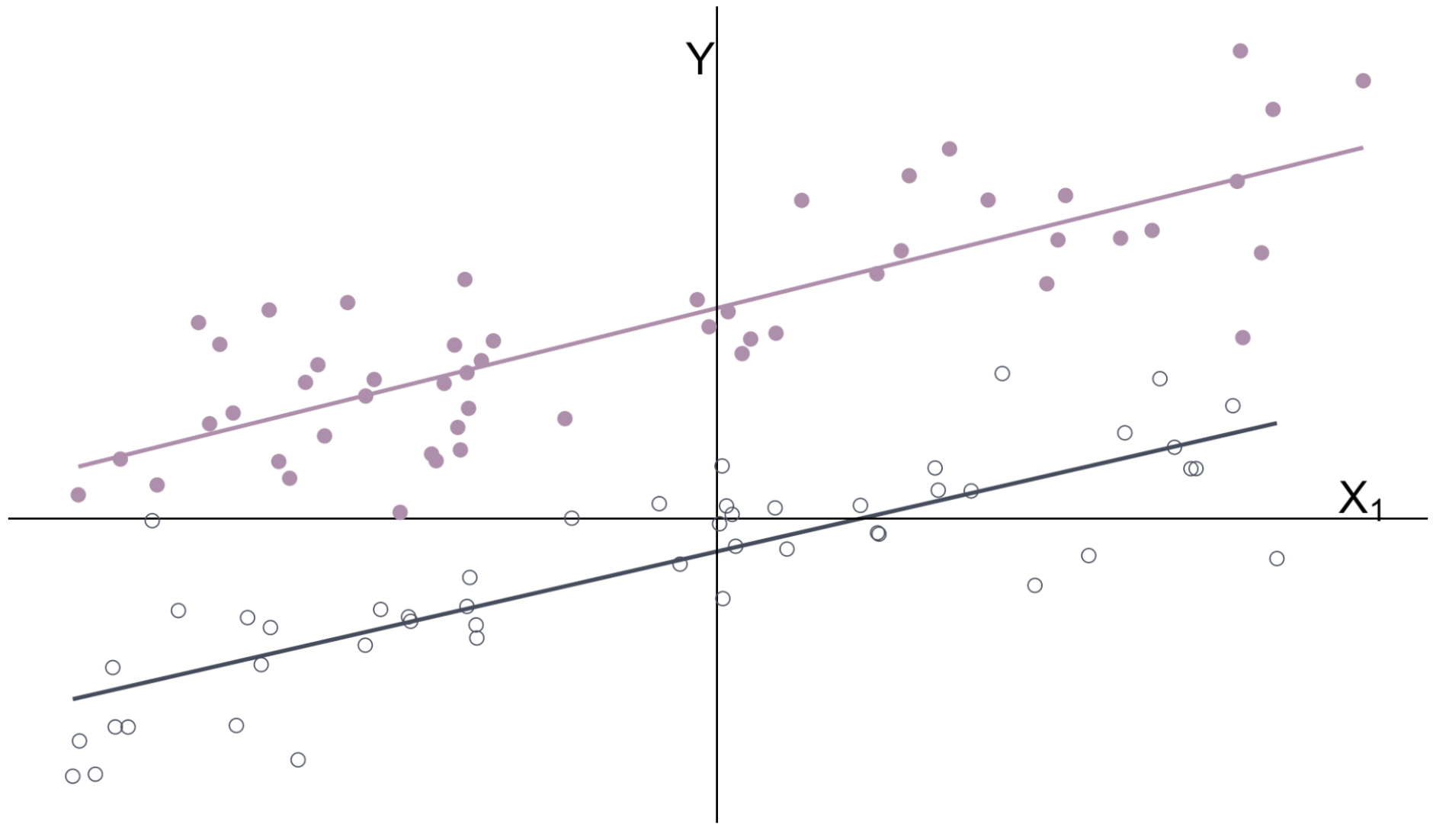
Omitted Variable Bias Example
Omitted variable bias
Ex. Imagine a population model for the amount individual \(i\) gets paid
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + \beta_2 \text{Male}_i + u_i \]
where \(\text{School}_i\) gives \(i\)’s years of schooling and \(\text{Male}_i\) denotes an indicator variable for whether individual \(i\) is male.
Interpretation
- \(\beta_1\): returns to an additional year of schooling (ceteris paribus)
- \(\beta_2\): premium for being male (ceteris paribus)
If \(\beta_2 > 0\), then there is discrimination against women.
Omitted variable bias
Ex. From the population model
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + \beta_2 \text{Male}_i + u_i \]
An analyst focuses on the relationship between pay and schooling, i.e.,
\[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + \left(\beta_2 \text{Male}_i + u_i\right) \] \[ \text{Pay}_i = \beta_0 + \beta_1 \text{School}_i + \varepsilon_i \]
where \(\varepsilon_i = \beta_2 \text{Male}_i + u_i\).
Omitted variable bias
We assumed exogeniety to show that OLS is unbiased.
Even if \(\mathop{\mathbb{E}}\left[ u | X \right] = 0\), it is not necessarily true that \(\mathop{\mathbb{E}}\left[ \varepsilon | X \right] = 0\)
- If \(\beta_2 \neq 0\), then it is false
Specifically, if
\[ \mathop{\mathbb{E}}\left[ \varepsilon | \text{Male} = 1 \right] = \beta_2 + \mathop{\mathbb{E}}\left[ u | \text{Male} = 1 \right] \neq 0 \]
Then, OLS is biased
Omitted Variable Bias
Let’s try to see this result graphically.
The true population model:
\[ \text{Pay}_i = 20 + 0.5 \times \text{School}_i + 10 \times \text{Male}_i + u_i \]
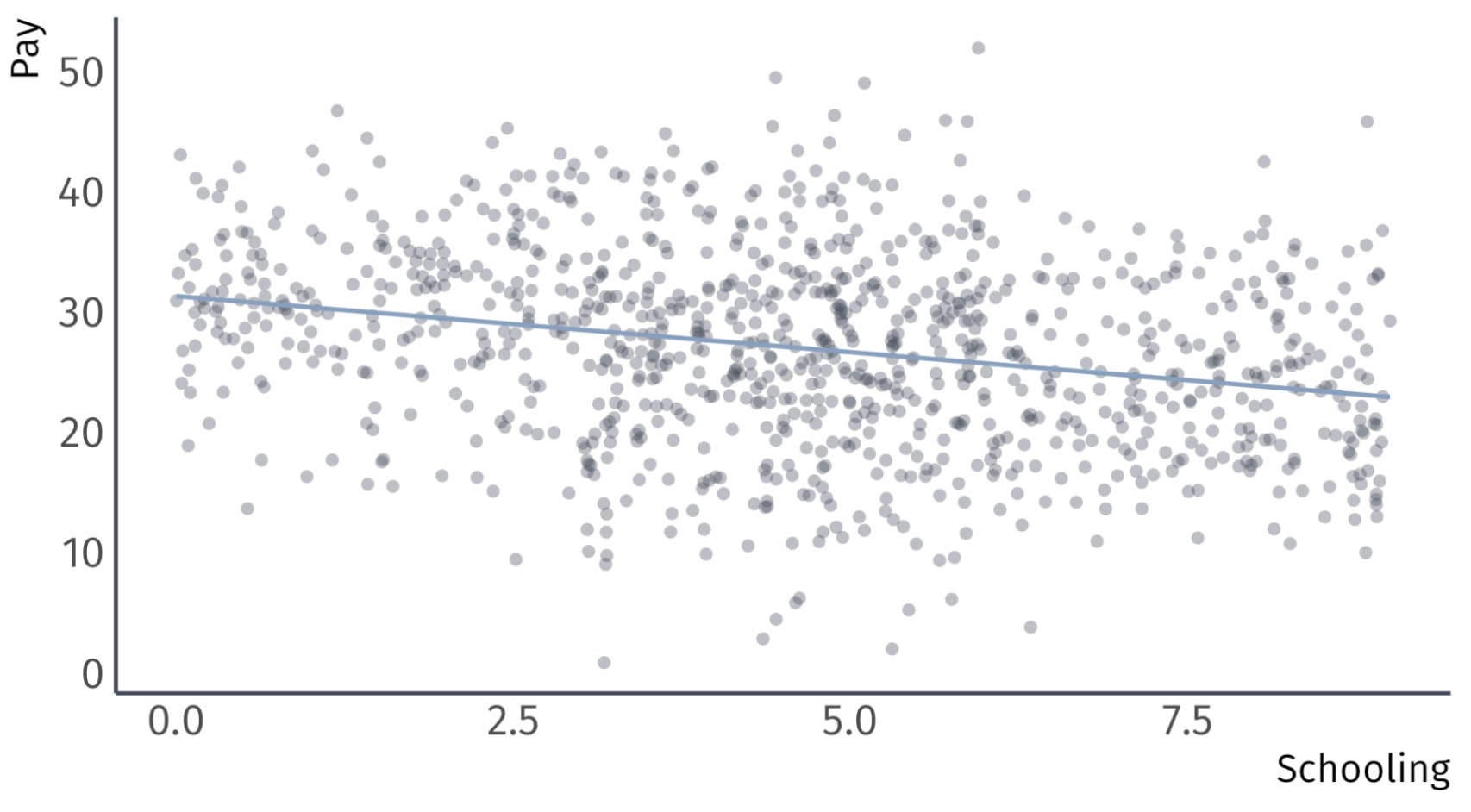
The regression model that suffers from omitted-variable bias:
\[ \text{Pay}_i = \hat{\beta}_0 + \hat{\beta}_1 \times \text{School}_i + e_i \]
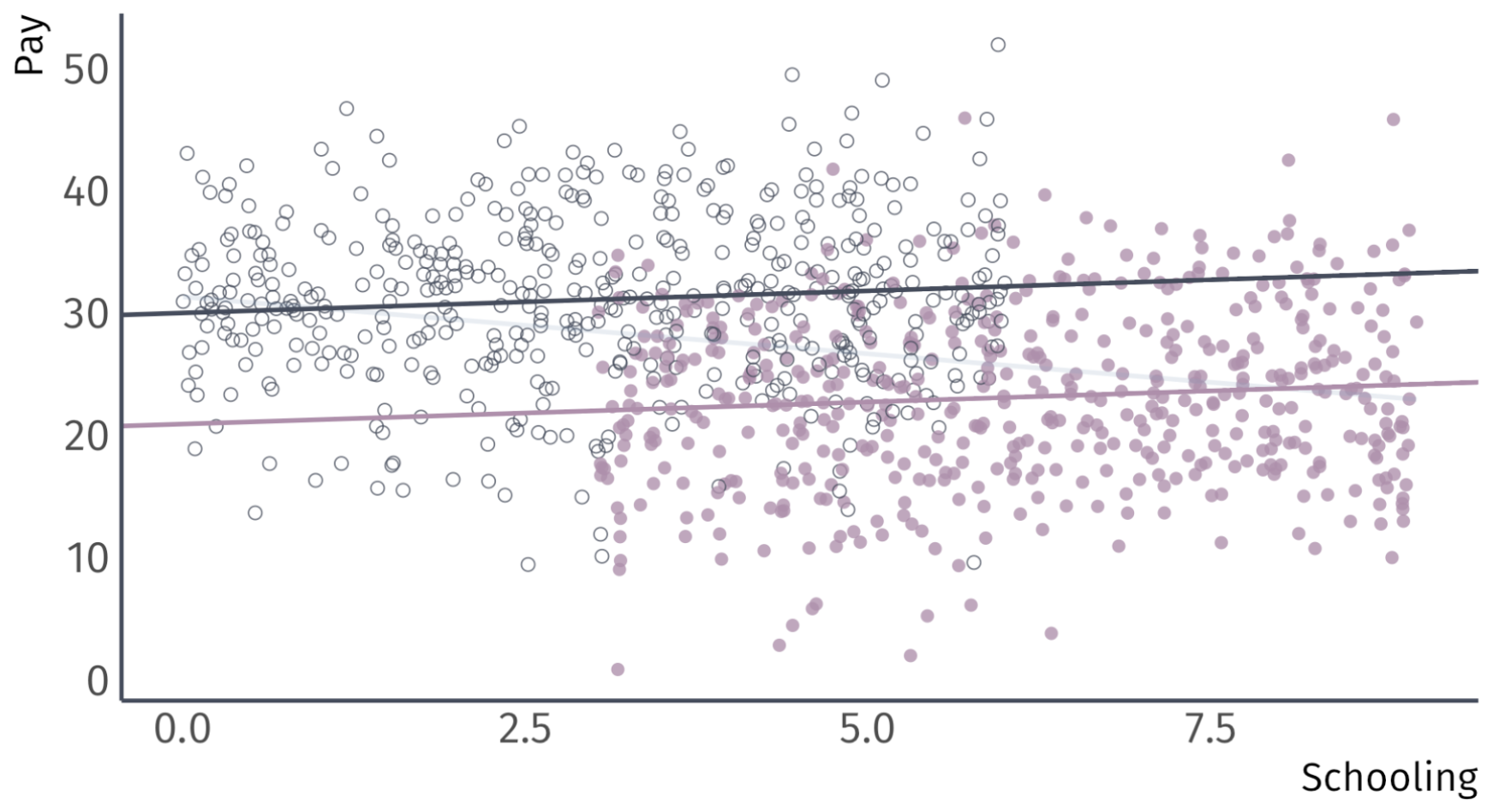
Suppose that women, on average, receive more schooling than men.
Omitted Variable Bias
True model: \(\text{Pay}_i = 20 + 0.5 \times \text{School}_i + 10 \times \text{Male}_i + u_i\)
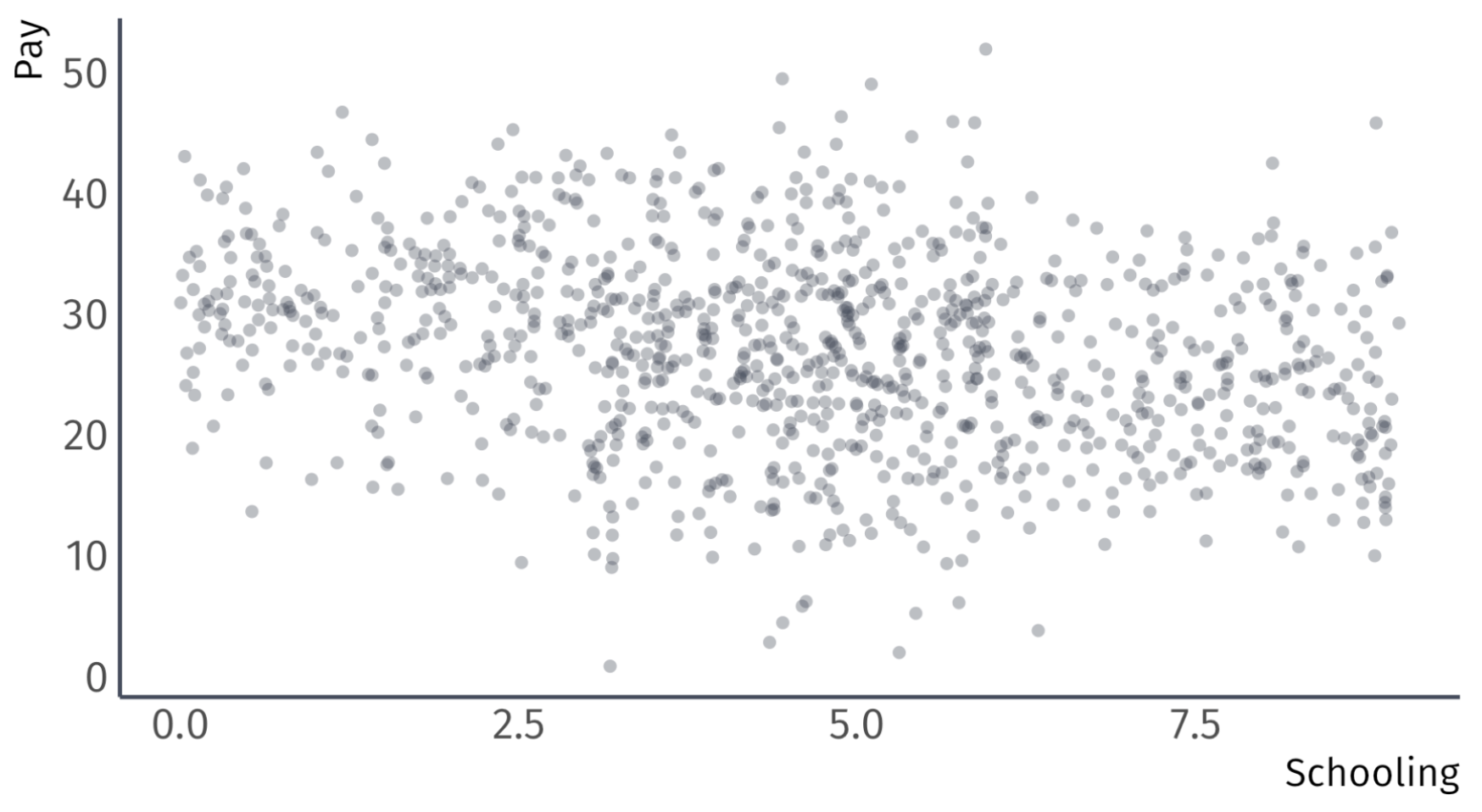
Omitted Variable Bias
Biased regression: \(\widehat{\text{Pay}}_{i} = 31.3 - 0.9 \times \text{School}_{i}\)
Omitted Variable Bias
Recalling the omitted variable: Sex (female vs male)

Omitted Variable Bias
Recalling the omitted variable: Sex (female vs male)
Omitted Variable Bias
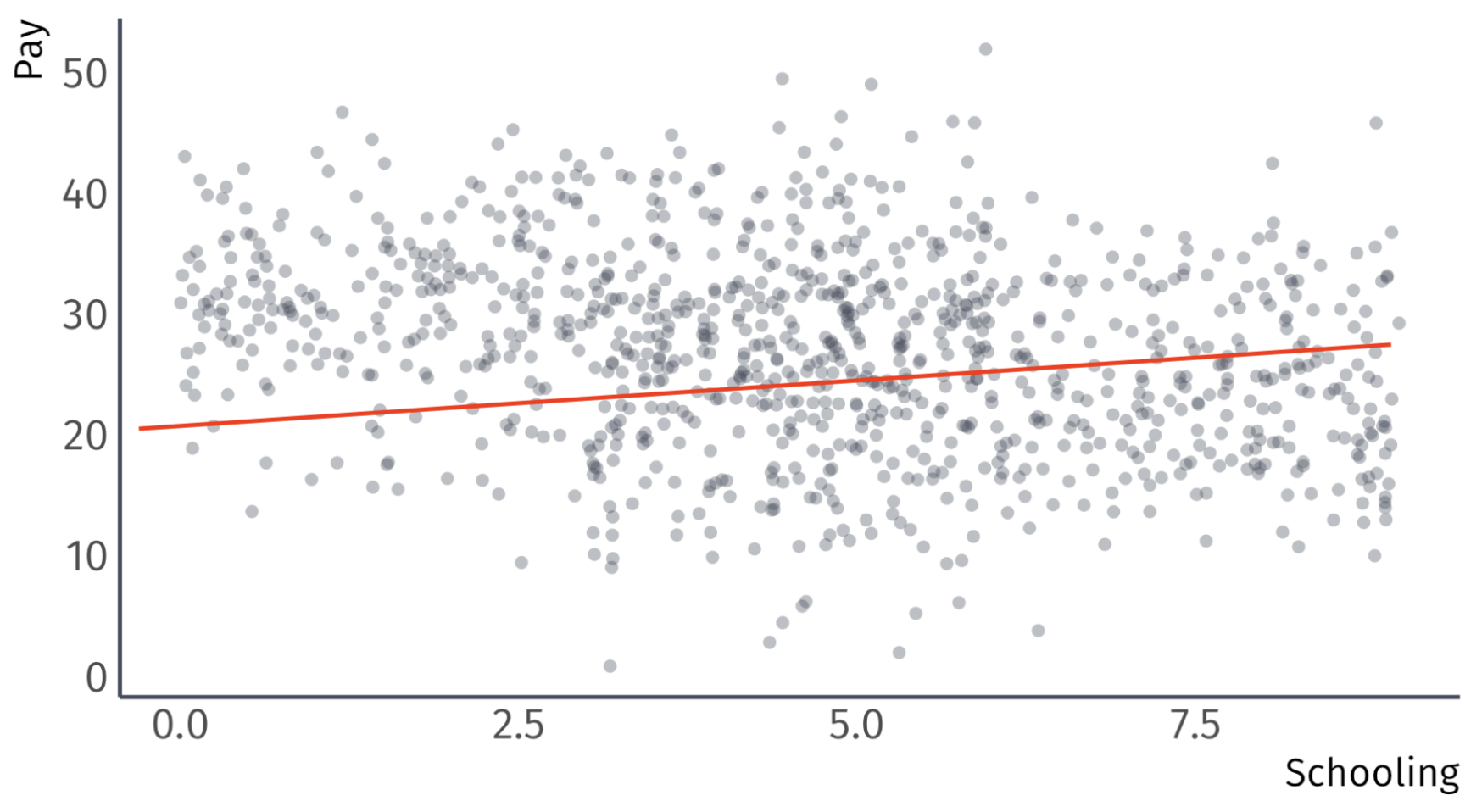
Unbiased Regression:
\[ \widehat{\text{Pay}}_{i} = 20.9 + 0.4 \times \text{School}_{i} + 9.1 \times \text{Male}_{i} \]
Interactive Relationships
Motivation
Regression coefficients describe average effects. But for whom does on average mean?
Averages can mask heterogeneous effects that differ by group or by the level of another variable.
We can use interaction terms to model heterogeneous effects, accommodating complexity and nuance by going beyond “the effect of \(X\) on \(Y\) is \(\beta_1\).”
Interaction Terms
Starting point: \(Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + u_i\)
- \(X_{1i}\) is the variable of interest
- \(X_{2i}\) is a control variable
A richer model: Interactions test whether \(X_{2i}\) moderates the effect of \(X_{1i}\)
\[ Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \beta_3 X_{1i} \cdot X_{2i} + u_i \]
Interpretation: The partial derivative of \(Y_i\) with respect to \(X_{1i}\) is the marginal effect of \(X_1\) on \(Y_i\):
\[ \color{#81A1C1}{\dfrac{\partial Y}{\partial X_1} = \beta_1 + \beta_3 X_{2i}} \]
The effect of \(X_1\) depends on the level of \(X_2\) 🤯
EC320, Lecture 07 | Categorical Vars and Interactions