Contemporary Models and Underdevelopment

EC 390 - Development Economics

Jose Rojas-Fallas

2025

Contemporary Models

So far we have seen that development is possible but difficult to achieve

The theory models we have seen use very strict assupmtions

• This is done to simplify the model and bring it down to a handful of variables that can change
• However the world is not simple

Newer theories relax some of these assumptions

• Perfect information
• Insignificance of externatilities
• Uniqueness/optimality of equilibria

Contemporary Models

These models attempt to incorporate more realistic observations of the developing world

A major theme is the inclusion of:

1. Binding Constraints

2. Coordination of Economic Agents

Contemporary Models

These models attempt to incorporate more realistic observations of the developing world

A major theme is the inclusion of:

1. Binding Constraints

• The main thing holding you back from growth

• If this limitation was to be relaxed, we would see accelerated growth (or an increased amount in whatever target we have)

2. Coordination of Economic Agents

Contemporary Models

These models attempt to incorporate more realistic observations of the developing world

A major theme is the inclusion of:

1. Binding Constraints

• The main thing holding you back from growth

• If this limitation was to be relaxed, we would see accelerated growth (or an increased amount in whatever target we have)

2. Coordination of Economic Agents

• A participant that chooses an action to maximize an objective

  • Firms, Workers, Consumers, Government Officials, etc.

Coordination Failure

Important Terms

Complementarity:

• An action taken by an agent, that increases the incentives for other agents to take similar actions

Coordination Failure

• A situation where the inability of agents to coordinate their behavior leads to an outcome that leaves everyone worse off than in an alternative situation that is also an equilibrium

Coordination Failure is essentially where agents do not work optimally together to reach the best possible outcome

Expectations

Let’s quickly introduce the important economic concept of Expectations

• Agents hold beliefs of what they think will happen

  • You expect that studying hard will improve your grades
  • You expect the empty restaurant will not be good

• These beliefs then shape your behavior

  • You study more
  • You go eat somewhere else

Complementarities

Expectations are an important component of complementarities

Complementarities will often involve investments where returns depend on other investments being made

• An important example is the presence of firms using special skills by agents and those agents acquiring those skills

• Later we will see a model that directly deals with worker skills complementing each other in production

Firms will not enter a market or locate somewhere if workers do not possess the skills the firms need, but workers will not acquire those skills if there are no firms to employ them

Coordination Between Agents

Coordination gets more difficult/unlikely as the number of agents increases

There can also be added limitations to coordinating behavior

• Agents may not be able to coordinate at all Where-to-Meet Dilemma

• Even if agents can coordinate, it may be difficult to convince them to

Price of Fish Example

Reading on Site

• Central Issue: Fishermen in India were not sure what the local prices were
  • A good catch might not fetch a lot of money if a fisher man chooses a saturated market
  • This led to surpluses and shortages
  • Coordination Failure

Price of Fish Example

Central Issue: Fishermen in India were not sure what the local prices were

• The most basic supply and demand curves require full information for all agents
• Without information, volatility and uncertainty enter the market
• The fishermen have no information on the local prices, and they were not sure where to sell
• This leads to volatile prices in the market
• With cell phones, information became accesible
• Cell phones also allowed them to coordinate
• “Law of One Price” emerged

Price of Fish Example

How did cellphones allow agents to overcome the coordination failure?

• They allowed fishermen to communicate with buyers and other sellers
• They could call a number of markets and find out where the price was highest
• Generally aware of where buyers had high Willingness to Pay
• Sellers were able to spread out across the different markets in an optimal way
• Eliminated inefficiencies like guessing

Cellphones made markets more efficient

Everyone benefited: Profits rose by 8% and prices fell by 4%

There was economic growth stemming from coordination

Multiple Equilibria

How Can There Be More Than One?

Basically, reflects a more (but not entirely) realistic possibility of outcomes

We will be matching expectations to reality

• Recall that expectations are not necessarily reality but they do inform it

• Multiple Equilibria is the condition where more than one equilibria exists

• These equilibria may sometimes be ranked, in the sense that one is preferred to another

• The standard diagram takes an S-shape around a 45 degree line

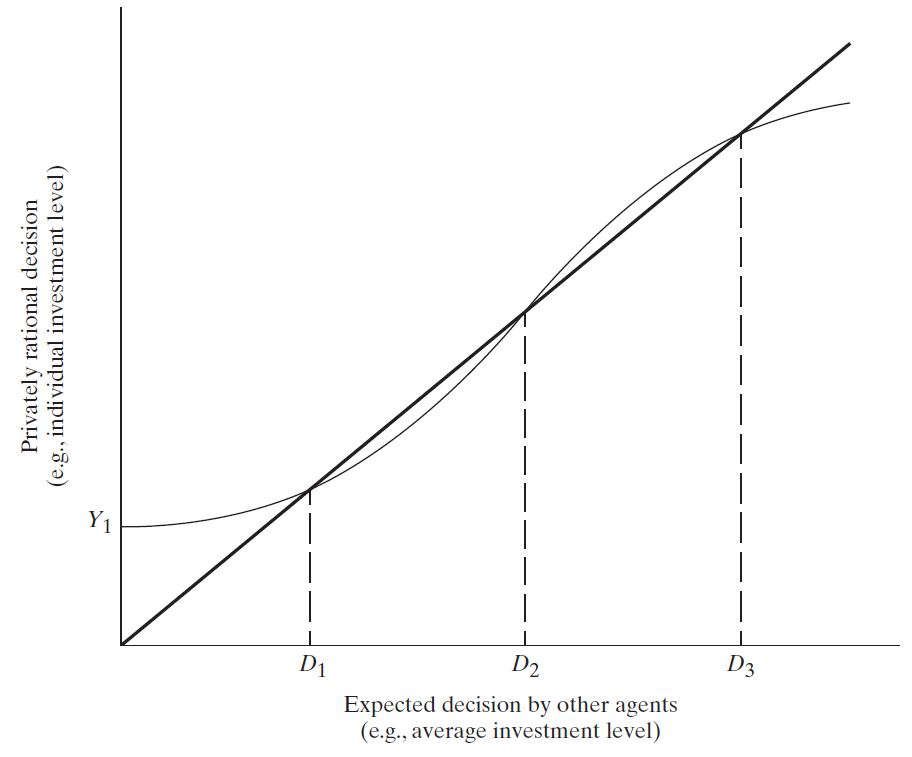
Multiple Equilibria

Components of the S-Diagram

Wavy Line Private Decision Function

• Tells us the best decision an individual can make given decisions of all other agents

45 Degree Line

• Shows all points where an individual’s decision is exactly the same as the expected decision of all other agents

Multiple Equilibria

Finding the Equilibria

• We identify where the private decision function is the same as the 45 degree line
  • These points are where it is privately optimal to do what other agents are doing
  • No agent has an incentive to deviate
• But there is stability to consider as well

Stable vs Unstable Equilibria

Stable Equilibria

• An equilibrium is stable if it is the case that if we were to move away from it, then agents will eventually end back at that equilibrium

Unstable Equilibria

• An equilibrium is unstable if it is the case that if we were to move away from it, then agents will take actions that make it move further away from it

How can we tell if an equilibrium is stable/unstable?

• If the S-Curve is flatter than the 45-Degree line than it is stable

• If the S-Curve is steeper than the 45-Degree line than it is unstable

In this previous example, \(D_{1}\) and \(D_{3}\) are stable

And \(D_{2}\) is unstable

Big Push

This model helps us understand something like perpetual poverty or the middle income trap

Take for example a nation with a low average investment

• If nothing is done, investment will simply return to \(D_{1}\) and there will be less and less economic activity
  • Recall what our previous models infer about low investments low output
• If investment could be increased beyond the intermediate point \(D_{2}\), then these models predict that investment would eventually end up at \(D_{3}\)

Examples of a Big Push

Intestinal works are prevalent among children in the poorest of developing countries

• Worms lead to sickness
• Sickness means missed school or missed work
• Worms spread from children to children in several ways
• Coordination Failure: If no one treats their child (or if they are unable to), why should I treat mine?
• Studies have shown that deworming medicine leads to a large increase in school attendance in Kenya, even among untreated children

Multiple Equilibria Problems

There are several other problems with multiple equilibria to consider

1. Firm Incumbency

2. Behaviour and Norms

3. Linkages

Multiple Equilibria Problems

1. Firm Incumbency

• Existing firms have an advantage over new firms
• This may be true even if they have relatively worse technology
• Take the entry of a modern firm, with better technology
• Even if the new firm has better tech, they run up against an economies of scale problem
• The local firm produces more output, so their per-unit cost is lower
• A new firm cannot just match production yet, even though they may produce output more efficiently
• Older firms can adjust and obtain the more efficient tech, but can they?
• If capital markets are poor, then they cannot invest properly and the economy is stuck with the inefficient production

2. Behaviour and Norms

3. Linkages

Multiple Equilibria

1. Firm Incumbency

2. Behaviour and Norms

• Movement to a better equilibrium can be especially difficult when there are many agents to consider

• Some agents may have different and selfish incentives that make them act in corrupt ways

• Imagine how difficult it is to change someones mind from say corruption to a cooperative nature where working together benefits all

3. Inequality

Multiple Equilibria Problems

1. Firm Incumbency

2. Behaviour and Norms

3. Linkages

• A traditional view has been that some inequality may enhance growth because the savings of the rich are higher than those of the poor

• But in reality the poor save more than we think, or at the very least they do when we consider savings as investments in things like health, children’s education, and home improvements

• Even more importantly, in high inequality settings, the poor may not be able to get loans due to their lack of wealth

  • With lack of access to credit, they may not be able to get loans that finance productivity increasing investments (efficient capital, educational investment, etc.)

O-Ring Theory

Introduction

This model leans in on complementarities in production in a strong way

• The notion is that modern production (comparative to tradiotional crafts production) requires many activities be done well together in order for any of them to amount to a high value

The name comes from the unfortunate 1986 Challenger disaster where one small and inexpensive part (the O-Ring) failed and caused the space shuttle to explode

Key Feature - Complementarities Among Inputs

Start by thinking of the model as describing what goes on inside a firm, but we can extend this to an industry or sector of the economy

• Suppose that production is broken down into \(n\) tasks
• For simplicity, we say that these tasks are ordered by the required level of skill to complete them, \(q\), where \(0 \leq q \leq 1\)
  • The higher the skill, the higher the probability of it being “successfully completed”
• The production function is a simple one:
  • Output is given by multiplying the \(q\) values of each \(n\) tasks togehter, and this is then multiplied by a term \(B\) that is just a production scalar

O-Ring Production

\[ BF(q_{i},q_{j}) = q_{i}q_{j} \]

Let’s make a simplifying assumption that \(B = 1\) so then we just have \[F(q_{i},q_{j}) = q_{i}q_{j}\]

Now let’s introduce other assumptions

• Firms are risk-neutral
• Labor markets are competitive
• Workers supply labor inelastically

risk neutral: Firms behae as if it maximizes expected profit ignoring variance or uncertainty

O-Ring Production

One of the most prominent features of this type of production function is something called

Positive Assortative Matching

• This means that workers with high skills will work together and workers with low skills will work together

• Extending this thought to the comparison of economies, it predicts that high-value products will be concentrated in countries with high-value skills

• But how do firms attract more productive workers?

Positive Assortive Matching

How do firms attract higher skill workers?

In competitive markets, worker pay is determined by how productive you are

• A firm with a higher-productivity worker can afford the higher wage (why?) and is willing to bid higher to attract more high-skill talent
  • The value of the output will be higher with two productive workers than if they would to “mix” skill levels
• By making higher value outputs, they have higher returns which in turn become higher wages
• This leads to concentration of high-skill workers in high-value firms

This result indicates that firms and workers can fall into a trap of low skill and low productivity while some are able to “escape” into higher productivity

Positive Assortive Matching Example

Let’s look at a numerical exmaple to show this behavior.

• Suppose there are six total workers: three have skill level equal to 0.4 while the other three have skill level equal to 0.8.

• Following O-Ring theory, workers will be grouped up together in equilibrium

• Now suppose that one of the low-skill workers increases their skill level to 0.5 (likely through training) and at the same time, a high-skill worker increases their skill level to 1.0

  • In both cases there is a 25% increase in quality of one worker in both firms

• What does this mean for productivity growth in both firms?

Positive Assortive Matching Example

Calculate the growth in productivity of both firms

Lower-Skill Firm

• First Production Level

\[ (0.4)(0.4)(0.4) = 0.064 \]

• Second Production Level

\[ (0.4)(0.4)(0.5) = 0.080 \]

• Change in Production

\[ 0.080 - 0.064 = 0.016 \]

\[ 0.016/0.064 = 0.25 \]

Higher-Skill Firm

• First Production Level

\[ (0.8)(0.8)(0.8) = 0.512 \]

• Second Production Level

\[ (0.8)(0.8)(1.0) = 0.640 \]

• Change in Production

\[ 0.640 - 0.512 = 0.128 \]

\[ 0.128/0.512 = 0.25 \]

Positive Assortive Matching Example

So both firms increase their productivity by 25%.

However, the higher-skill firm saw a point value increase of 8 times as much as the lower-skill firm

With higher productivity come stronger incentive to draw in higher-skill talent and pay more to get other high-skill individuals

Or equally, upgrade skills among existing high skill workers

O-Ring Model Strong Assumptions

This model relies on some rather strong assumptions

1. Workers must be sufficiently imperfect substitutes for each other

2. There must be sufficient complementarity of tasks

O-Ring Model Strong Assumptions

1. Workers must be sufficiently imperfect substitutes for each other

Suppose that there are two skill levels \(q_{L}\) and \(q_{H}\) and that we can say \(q_{H} = 2q_{L}\)

• Each \(q_{H}\) earns twice as much as each \(q_{L}\)

• But we can perfectly replace every \(q_{H}\) worker with two \(q_{L}\) workers with no other change necessary

• We can make no predictions about what combination of workers a firm or economy will use which implies we cannot learn anything about low-skill level equilibrium traps

2. There must be sufficient complementarity of tasks

O-Ring Model Strong Assumptions

This model relies on some rather strong assumptions

1. Workers must be sufficiently imperfect substitutes for each other

2. There must be sufficient complementarity of tasks

Suppose that there are two tasks needed to complete an output and they are indexed by \(g\) and \(h\) but there is no complementary between them

Let a \(q_{H}\) worker be hired to complete \(g\) task and \(q_{L}\) worker completes \(h\) task, so we get

\[ F(q_{H},q_{L}) = g(q_{H}) + h(q_{L})\]

• Because a firm can only higher one type of worker for each task, there is no possible substitution

• However, because there is no complementarity, firms cannot optimize on skill so there is no strategic sorting

Implications of the O-Ring Theory

• Firms tend to employ workers with similar skills for their various tasks
• Workers performing the same task earn higher wages in a high-skill firm than in a low-skill firm
• Because wages incres in skill \(q\) at an increasing rate, wages will be more than proportionally higher in developed countries
• There are complementarities in investing in own skills
  • If others around you have higher average skills, you have a greater incentive to acquire more skills
• An economy can get caught in economy-wide, low-production-quality traps

Hausmann-Rodrik-Velasco Growth Diagnostics Framework

HRV Growth

Hausmann-Rodrik-Velasco (HRV) attempt to identify the greatest hindrance to growth for each developing nation

• Broadly speaking, low growth is caused by low return on investment or a high-cost of borrowing
  • Low returns on investment are the result of poor productive capability or low returns due to institutional failure
• HRV propose a decision tree framework to focus on a country’s most binding constraints on economic growth
• By targeting the most binding constraint produces advangates over other approaches to policy selection

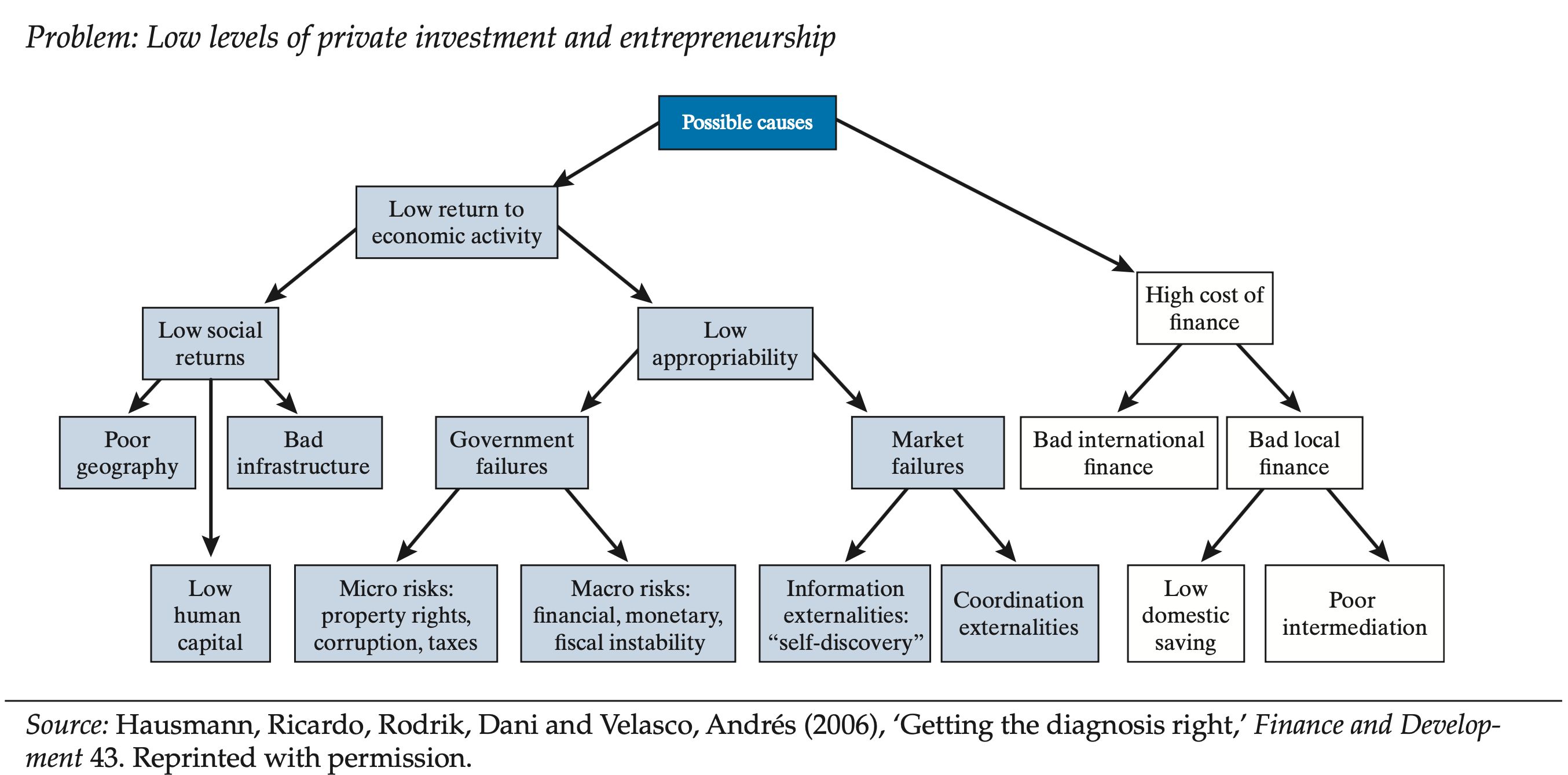
HRV - Four Principles of Differntial Diagnosis

1. The Shadow Price of the Constraint is High

2. Movements in the constraint produce significant movement in the objective

3. People attempt to overcome or bypass the constraint

4. Agents less intensive in a binding constraint are more likely to thrive

HRV - Four Principles

1. The Shadow Price of the Constraint is High

A Binding Constraint on growth is one where relaxing it would yield large benefits. Meaning its shadow price (the implicit value of easing the constraint) is high

• If something is scarce because of low supply rather than low demand, it is likely a true contraint
  • Ex: If credit is limited and interest rates are high, even though many agents want to borrow, financial access is binding
  • If little borrowing occurs because agents do not see high returns, then fincance is not a binding issue
• Clues come from high observed returns, rationing, congestion, or other indicators that an input is in short supply

If we could ease this bottleneck, would growth respond strongly?

If yes, then it is probably a key constraint

HRV - Four Principles

2. Movements in the constraint produce significant movement in the objective

If something is truly binding, then changes in it should move the economy’s main outcomes.

• If we suspect that limited access to credit constrains investment, then lowering real interest rates or improving access to loans should incrase investment
• The relationship should be clear and consistent
  • When the constraints bites harder, outcomes worsen
  • When it eases,outcomes should improve

This principle checks the sensitivity of the constraint.

If chaniging the variable does not affect performance much, it is probably not the real bottleneck

HRV - Four Principles

3. People attempt to overcome or bypass the constraint

Economic actors do not passively accept constraints, they adapt or find workarounds.

• When things fail, agents might invest or find in alternatives
  • The power grid fails often, so agents invest in generators to overcome unreliable electricity
  • If crime is high, agents might invest in private security
  • If taxes are too much or unreasonable, business might shift toward cash only
• By observing coping mechanisms, we can better identify what the economy’s main problems are

If agents spend a lot of effort or resources getting around certiain limitations, that limitation is likely binding

HRV - Four Principles

4. Agents less intensive in a binding constraint are more likely to thrive

If a constraint is binding, agents that participate less or are less exposed to it will perform better.

• If a contraint does not directly (or it is less prevalent) affect your action, then the agent is not as limited
  • Ex: If infrastructure is the issue, exporting firms near a port may grow faster than inland producers
  • Ex: If political corruption is the main concern, then agents that are politically connected will succeed while others stagnate

This principle checks the variation within the economy, which agents grow and which do not?

The presence (or absence) of thriving sectors reveals a lot about what is holding back the rest of the economy.

Why are the successes succeeding, and the failures failing.